Znajdź pierwiastki równania kwadratowego. curiosis: Witam. Szukałem tego zadania na forum i nie znalazłem, a miałem sprawdzian i to zadanie mam zrobione na 0pkt na 3 możliwe i chciałbym was poprosić o pomoc. (treść niestety z pamięci, ale mam nadzieję, że zrozumiecie mnie ) Zad. Ilość rozwiązań ze względu na parametr "p" x²−2|x|+3p Jak już ktoś się za to zabierze to nie musi dokładnie wszystkiego opisywać, z pewnością skumam xD Dziękuję za poświęcony czas

Adamm: x²−2|x|+3p=0 ?

Jerzy: podstaw: t = Ix| i warunek : t ≥ 0 masz rówenanie: t² − 2t + 3p = 0 ... i prowadź analizę.

'Leszek: Aby sprawdzic czy wszystkie warunki wykorzystales wykonaj wykresy f(x) = x² − 2x oraz g(x) = −3p i zobaczysz w ilu punktach dla roznych p zachodzi f(x) = g(x)

'Leszek: Sorry ,powinno byc oczywiscie f(x) = x² − 2 |x| ,

curiosis: Możliwe, że to miało być, narysować wykres x²−2|x| i potem sprawdzić dla jakich p ile jest rozwiązań, ale rozumiem już o co chodzi, dziękuję

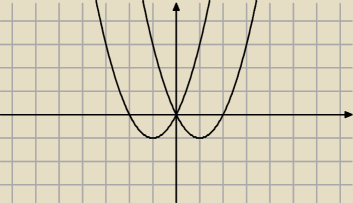
piotr: i widać, że: dla p∊(−∞;0) mamy 2 rozwiązania dla p=0 mamy 3 rozwiązania dla p∊(0;1/3) mamy 4 rozwiązania dla p=1/3 mamy 2 rozwiązania dla p∊(1/3; +∞) ni ma rozwiązań

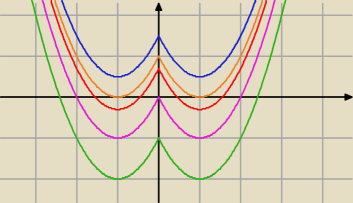
===: zauważ, że Twoja f(x) jest parzysta (oś 0y jest jej osią symetrii)

curiosis: Jak Piotrze wyznaczyłeś te p? Mi się wydawało, że od dołu się jedzie i np. dla 3p<−1 brak rozwiązań 0.o

curiosis: up

curiosis: up