Dla jakich wartości parametru m równanie... Rev: Dla jakich wartości parametru m równanie: a) |x+2|=m²−m ma dwa ujemne rozwiązania b) |x−2|=(m+1)/(m−2) ma dwa rozwiązania różnych znaków Pozdrawiam i mam nadzieję że ktoś pomoże

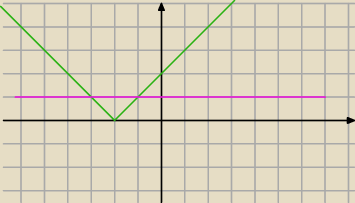
Jerzy: a) Różowa linia, to prosta: y = k , stal jakie kusi być k , potem rozwiąż równanie: m² − m = k

Jerzy: ... a ściślej nierówność: k₁ ≤ m² − m ≤ k₂

Rev: A co w tym zapisie jest k1, a co k2? I jeszcze mam pytanie dlaczego prosta k ma wartość y=1? Chyba że po prostu czegoś nie zrozumiałem

Jerzy: Oznaczamy różową prostą y = k Ustal w jakim zakresie różowa prosta przecina zieloną w dwóch punktach o ujemnych odciętych.

Rev: Ok, to już wiem. Teraz kwestia taka, że nie wiem w jaki sposób powinienem obliczyć miejsce przecięcia z osią oy, wiedząc że x+2=m²−m.

Adamm: y=k to bardziej rodzina prostych spełniających równanie |x+2|=k z dwoma ujemnymi rozwiązaniami nie jest to jakaś konkretna prosta z tego dowiesz się w jakim przedziale powinny znajdować się wartości m²−m drugie robisz analogicznie

Adamm: np. z rysunku widzisz że k∊(0;2) stąd 0<m²−m<2 0<m(m−1) ∧ (m−2)(m+1)<0 m∊(−1;0)∪(1;2)

Rev: Już zrozumiałem, dziękuję bardzo za pomoc w rozwiązaniu.