Twierdzenie Lagrange TakieFajne: Czy może ktoś podać przykład takiej funkcji? Pokaż, przedstawiając odpowiedni przykład i rysunek wykresu funkcji ,że w tw. Rolle'a każde z założeń (o ciągłości , o różniczkowalności, o róności wartości na końcach przedziału)jest niezbędne.

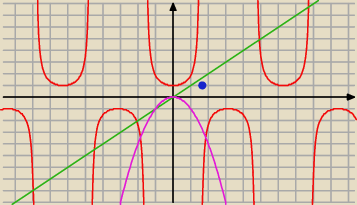
Adamm: tw. Rolle'a mówi nam że jeśli funkcja jest ciągła, na przedziale <a; b>, różniczkowalna na przedziale (a; b), to jeśli f(a)=f(b) to istnieje taki c∊(a; b) że f'(c)=0 jako przykład ciągłości można podać 1/cos(x) dla x∊<0;π/2) oraz 1 dla x=π/2 pomimo iż f(0)=f(π/2) oraz jest różniczkowalna dla (a; b) to nie spełnia warunku ciągłości, i jak widać, równanie nie zachodzi jako przykład różniczkowalności można podać x dla x≤0 oraz −x² dla x≥0 funkcja jest ciągła, różniczkowalna poza punktem x=0 oraz f(−1)=f(1), a mimo to nie istnieje taki c∊(−1; 1) że f'(c)=0 jako przykład równości, to dosyć łatwo jest wymyślić przykład chociażby ta nieszczęsna funkcja f(x)=x dla x od −1 do 1 jest różniczkowalna, jest ciągła, ale nie spełnia równości, i nie istnieje taki c że f'(c)=0