Oblicz promień okręgu opisanego na ośmiokącie foremnym. Patryk:

Patryk: Witam proszę o pomoc

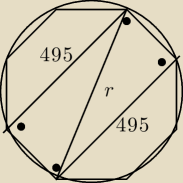
Mila: 495 to co oznacza?

Patryk: Długość najdłuższego boku prostokąta.

g: 495² = 2r²(1−cos(3*360/8)) 3*360/8 = 135 cos(135) = −sin(45) = −√2/2

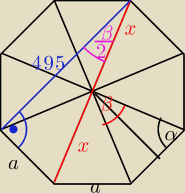
po prostu Michał: r = 2x

	180−β
2α + β = 180 −−−> α =
	2

	β
zatem tamten kat u gory = 90 − α =
	2

	β		a
tg		=
	2		495

oraz co wiemy, o czym sie czesto zapomina? ze kat pelny ma 360^o, zatem 8β = 360 −−> β = 45

	a   2
cos α =		(wiemy, ze α = 180−45 = 135)
	x

zatem

	a
cos 135 =
	2x

	√2
cos(135) = cos(90+45) = − sin (45) = −
	2

	√2		a
−		=
	2		2x

wyznacz np. a a nastepnie z pitagorasa w tamtym trojkacie a² + 495² = (2x)² (gdzie 2x = r) − u Ceibie)

Patryk: Czy "r" wyjdzie po zaokrągleniu ≈349,7175 ?

'Leszek: Jest to osmiokat foremny : β = 360°/8 = 45° a= 495*tg (β/2) Z tw.Pitagorasa 4x² = a² + 495² ⇒r = (495/2)*√1 + tg²(β/2)

Pitol: ≥gh∉