Geometria Analityczna
Dominik: wyznacz wszystkie wartosci parametru k,dla ktorych wierzcholek paraboli o rownaniu
y=x2−2kx+2k2−4k+k nalezy do kola o srodku S=(3,2) i promieniu √5.
Proszę o pomoc..
10 maj 21:00
Leo: Oblicz współrzędne wierzchołka w zależności od parametru k i podstaw do równania okręgu
10 maj 21:10
Leo: Przy czym (x−3)2+(y−2)2≤5
10 maj 21:11
Dominik: no właśnie z tym pierwszym mam problem. Dalej jakoś pójdzie

10 maj 21:11
Leo: P=−b/2a q=f(p)
10 maj 21:12
Dominik: p=k
q=−k2+4k−4 (wziąłem to z wzoru q=−Δ4a)
no i teraz podstawiam
(q−3)2+(p−2)2≤5 tak? Czy coś źle zrozumiałem
10 maj 21:14
Mila:
Wzór funkcji tak wygląda?
10 maj 21:15
Leo: Ja mam inne q ^^
10 maj 21:16
Dominik: no właśnie przez to q wychodzi mi jakiś mega długi wielomian i nie wiem co dalej z tym zrobić.
Dobra, sprobuje jeszcze raz bo jesli mam byc szczery to nie wiem jak wyglada f(p)

10 maj 21:18
Leo: Pierwszą współrzędną wierzchołka, Twoje p=k podstawiasz pod x bo zamiast f(x) szukasz f(p)
10 maj 21:19
Mila:
Dominik, podany wzór dziwny , przecież
....... −4k+k=−3k, po co tak podają, może źle przepisałeś?
10 maj 21:19
Dominik: A mógłbyś napisać jakie Tobie wyszło? Bo nie chce znowu jakiejś głupoty napisać i tylko
sprawdzę czy tyle samo

10 maj 21:20
Leo: q=k2−3k
10 maj 21:21
Dominik: Mila, wydaje mi sie ze u ciebie sie coś źle wyświetla, bo nigdzie czegoś takiego nie ma. Chodzi
Ci o rownanie paraboli w treści?
10 maj 21:22
Dominik: No z f(p) wychodzi mi tyle samo, to znaczy, że w tym przyapdku nie mogę zastosować q=−Δ/4a?
Dlaczego?
Pytam bo nigdy bym nie wpadł na coś takiego.
10 maj 21:24
Mila:
y=x2−2kx+2k2−4k+k taki wzór paraboli ?
wg mnie zamiast ostatniego k powinna być liczba.
10 maj 21:29
Dominik: Owszem, mój błąd. Zamiast ostatniego k powinno być +4.
10 maj 21:31
Mila:
xw=k
yw=k2−2k2+2k2−4k+4=k2−4k+4=(k−2)2
(k−3)2+(k2−4k+4−2)2≤5⇔
(k−3)2+(k2−4k+2)2≤5⇔
k2−6k+9+k4+16k2+4−8k3+4k2−16k−5≤0
k4−8k3+21k2−22k+8≤0
W(1)=0
1 −8 21 −22 8 k=1
1 −7 14 −8 0
================
k4−8k3+21k2−22k+8=(k−1)*(k3−7k2+14k−8)
p(k)=(k3−7k2+14k−8), p(1)=1−7+14−8=0
1 −7 14 −8 k=1
1 −6 8 0
==============
k4−8k3+21k2−22k+8=(k−1)*(k−1)*(k2−6k+8)
dalej licz sam
10 maj 21:46
Dominik: No więc wyszło mi, że k=1 lub k=4 lub k=2. I to jest po zadaniu już?
Oraz czym sie różni ten sposób leo, ponieważ tutaj wykorzystałaś(?) (k−2)2 a Leo miał k2−3k
10 maj 22:10
Mila:
Leo liczył wg poprzedniego wzoru funkcji z godziny 21:00
(k−1)*(k−1)*(k2−6k+8)=(k−1)2*(k−2)*(k−4)
(k−1)2*(k−2)*(k−4)≤0⇔
k∊<2,4>∪{1}
Rysunek osi źle się edytuje.
Może w nowym wpisie będzie lepiej.
10 maj 22:17
Mila:
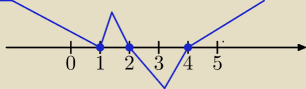
10 maj 22:20
Dominik: Dobra, juz wszystko rozumiem. To zadanie będzie mi się śniło po nocach...
10 maj 22:25



