Rozwiąż równanie kwadratowe Trębacz: |x²−4x|<4 mam problem z tym równaniem, otóż w książce nie ma odpowiedzi do tego zadania, a wyszło mi, że x∊(2−√2;2+√2)

AiO: prosze pokazac obliczenia

Krzysiek: x∊(2−2√2;2+2√2)\{2}

Adamm: jest źle

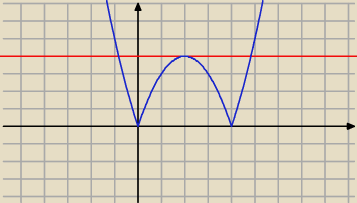
AiO: To jest rozwiazanie graficzne niebieski y=|x²−4x| i czerwony y=4

Trębacz: rozłożyłem nierówność do postaci |x(x−4)|<4; miejsce zerowe lewej strony to 0 i 4. 1. x∊(−∞;0) i x²−4x−4<0 x1=2−2√2 x2=2+2√2 x∊(2−2√2;0) 2.x∊<0;4) i −x²+4x−4<o x należy do zbioru pustego 3. x∊<4;+∞) i x²−4x−4<0 x1=2−2√2 x2=2+2√2 x∊<4;2+2√2) z 1 v 2 v 3 ⇒ x∊ (2−2√2;0) u x∊<4;2+2√2) na górze wkradły się małe błędy

Adamm: nadal jest źle dobrą odpowiedź podał Krzysiek

Trębacz: w takim razie błąd siedzi w 2 warunku zaraz poszukam go

relaa: |x² − 4x| < 4 −4 < x² − 4x < 4 0 < (x − 2)² < 8 x ≠ 2 ∧ |x − 2| < 2√2 ⇒ x ∊ (2 − 2√2 ; 2 + 2√2) \ {2}.

AiO: Skorzystaj tutaj z wlasnosci wartosci bezwzglednej |x|<a ⇔x<a i x>−a

Trębacz: znalazłem błąd w moim rozwiązaniu w 2 warunku Δ=0, miejsce zerowe=−2 −2<0⇒ rozwiązaniem jest cały przedział, i już się zgadza, tylko pytanie czy mój tok rozumowania jest dobry

AiO: Pomysl z rozpisaniem na przedzialy jest dobry