zad QWERTY: Napisz równania kierunkowe stycznych do danego okręgu o i nachylonych do osi OX pod kątem α, jeśli: ∨(x−1)²+y²=4 α=120 x²+y²−2x−3=0 a=1 ∧ b=0 ∧c=−3 r²=4 r=2 tg120=tg(180−60)=−√3 y=−√3+b √3+y−b=0 A=√3 B=1 c=−b d=r

	|√3*1+1*0−b|
2=
	√(√32)+(12)

	|√3−b|
2=
	2

|b−√3|=4 b−√3=4 ∨ b−√3=−4 b=√3+4 v b=√3−3 l₁:y=√3x+√3+4 l₂: y=√3x+√3−4 Dobrze

QWERTY:

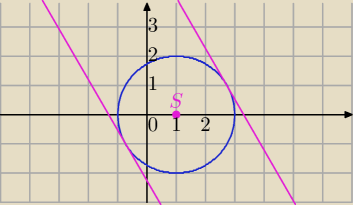
Mila: (x−1)²+y²=4 , S=(1,0), r=2 α=120^o, tg120^o=tg(180−120)=−tg60^o=−√3 Styczna: l: y=−√3*x+b odległość prostej od S=(1,0) jest równa 2 l: −√3*x−y+b=0

	|−√3*1−0+b|
d(l,S)=		=2⇔
	√(√3)2+12

|−√3+b|=2√4 |−√3+b|=4 −√3+b=4 lub − √3+b=−4 b=√3+4 lub b=√3−4}⇔ l₁: y=−√3*x+4+√3 lub l₂: y=−√3x−4+√3

ax: nie

QWERTY: Napisz równania ogólne stycznych do danego okręgu o i przechodzących przez punkt A, jesli o:x²+y²=4 A(6,−2) r=2 y=ax+b −2=6a+b −6a−2=b y=ax−6a−2 ax−y−6a−2=0

	|a*0+(−1)*0−6a−2|
2=
	√a2+(−1)2

nie wychodzi mi a₁ i a₂ prawidłowe

QWERTY:

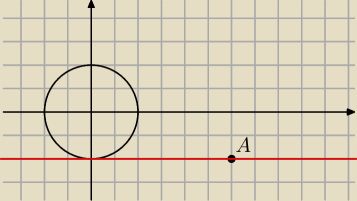
AiO: Widzisz z rysunku ze jedna styczna ma rownie y=−2 w postaci ogolnej y+2=0 natomiast druga prosta przechodzaca przez punkt A ma rownie y+2= m(x−6) mx−y−6m−2=0 czyli twoje

|−6m−2|
	=2 (*√m2+1
√m2+1

|−6m−2|= 2*√m²+1 (obie strony do potegi drugiej |−6m−2|²= 4(m²+1) (−6m−2)²= 4m²+4 36m²+24m+4= 4m²+4

	24		3
32m2+24m=0 ⇒m(32m+24)=0 ⇒m=0 lub 32m+24=0 ⇒m= −		= −
	32		4

	3
czyli masz m=0 to co napisalem wczesniej im=−
	4

Rownanie prostej sobie napisz

AiO: Poprawie czyli Twoje

|−6m−2|
	=2
√m2+1

Skrocilem w glowie sobie dzialanie i tak napisalem poprzednio

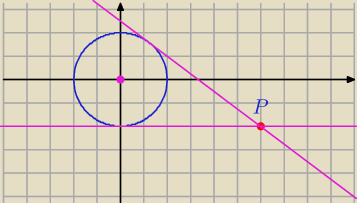
Mila: x²+y²=4 S=(0,0) , r=2, P=(6,−2) y=ax+b⇔−2=6a+b, b=−2−6a l: ax−y−2−6a=0

	|a*0−0−2−6a|
d(l,S)=		=2
	√a2+1

|2+6a|=2*√a²+1 |1+3a|=√a²+1 /² 1+6a+9a²=a²+1 8a²+6a=0 a(8a+6)=0

	3
a=0 lub a=−
	4

l₁: y=−2 ⇔y+2=0 lub

	3		3
l2: −		x−y−2−6*(−		)=0⇔
	4		4

	3		5
−		*x−y+		=0 /*(−4)
	4		2

l₂: 3x+4y−10=0

QWERTY: Bardzo dziękuje

Mila: a co z tym wynikiem z 20:46? zgadza się z odpowiedzią?

QWERTY: Jest dobrze

Mila: