Red: Narysuj na płaszczyźnie zespolonej 1 ≤ |jz−3|≤2 z = x+yj 1 ≤ |j*(x+yj)−3|≤2 1 ≤ |xj−y−3|≤2 √(−y−3)² + x² czy tak mam to dalej liczyć?

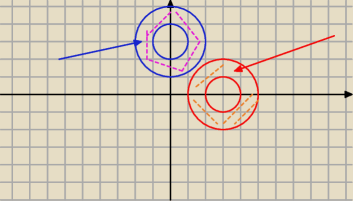
Adamm: jz to przesunięcie płaszczyzny o 90^o przeciwnie z ruchem wskazówek zegara 1≤|z−3|≤2 <− czerwony interpretacja to zbiór okręgów o środkach w punkcie 3, o promieniach od 1 do 2 1≤|jz−3|≤2 to ten sam obszar, ale przesunięty o 90^o zgodnie z ruchem zegara (względem środka układu współrzędnych) (na niebiesko)

Adamm: "ale przesunięty o 90o zgodnie z ruchem zegara" przeciwnie, co napisałem wyżej

Red: TO ja już nie wiem bo według mojego prowadzącego wynikiem jest pierścień o środku (0; −3 ) o promieniach 1 i 2

Adamm: no dobra, niektóre z wniosków były nieuzasadnione jz jest przesunięciem płaszczyzny o 90^o przeciwnie do ruchu zegara, to się nie zmieniło to co się zmieniło, to interpretacja która mówi że 1≤|jz−3|≤2 można traktować jako takie złożenie, i tak to narysować jz jest przesunięciem, więc odległość liczby przesuniętej jest taka sama jak oryginalnej, czyli |jz|=|z| korzystając z wniosku zapisujemy 1≤|z−3j|≤2 i tutaj już o niczym nie trzeba myśleć, |z−3j| to odległość 3j od z, a z nierówności wiemy że musi wynosić od 1 do 2 i masz swój pierścień

Red: a takie pytanie czemu punkt −1 jest wykluczony z tego obszaru?

Adamm: inna wersja, możesz myśleć o tym tak z'=jz i to jest to co narysowaliśmy, zbiór punktów z' by otrzymać z musimy podzielić przez j, czyli inaczej pomnożyć przez −j, czyli przesunąć nasz obszar o −90^o

Adamm: −1 jest wykluczony z obszaru bo nie spełnia nierówności nie rozumiem czemu zadane pytanie było takie konkretne

Red: Ok, dziękuje bardzo

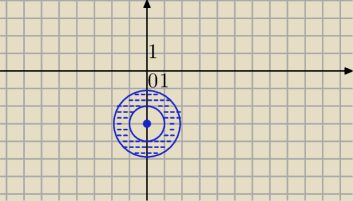
Mila: 1 ≤ |jz−3|≤2⇔ 1 ≤ |j*(z+3j)|≤2⇔1 ≤ |j|*|(z+3j)|≤2 1≤|z+3j|≤2⇔ 1≤|z−(−3j)|≤2