W pewnym trójkącie prostokątnym wysokość opuszczona z wierzchołka kąta prostego dzieli przeciw
prostokątna na odcinki o długości 3cm i 12 cm. Oblicz długość tej wysokości .
w podręcznikowych odpowiedziach pisze że wynik wynosi 6 cm
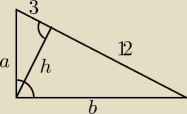Jak widać na rysunku: powstały 3 trójkąty prostokątne: duży o bokach a, b i 15, średni o bokach
h, b i 12 oraz mały na bokach a, h i 3. Dla każdego z nich należy zapisać równanie oparte na
twierdzeniu Pitagorasa:
a2 + b2 = 152
122 + h2 = b2
32 + h2 = a2
Zbudowaliśmy układ 3 równań z 3 niewiadomymi. Nie trzeba go całego rozwiązać, wystarczy do
pierwszego równania wstawić drugie i trzecie:
122 + h2 + 32 + h2 = 152
2 * h2 + 144 + 9 = 225
2 * h2 = 72 / :2
h2 = 36
h = 6
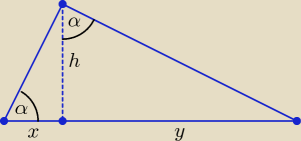
| h | y | |||
Z podobieństwa trójkątów: | = | ⇒ h2 = xy i h > 0 | ||
| x | h |