Jak oceniacie poziom tegorcznej matury rozszezronej ? MaturaR2017: Jak oceniacie poziom tegorcznej matury rozszezronej ?

Wielomian : Ujdzie

House: nie trudne

Wielomian : Kula pierwszy raz od dawna

MaturaR2017: dwa dowody ?

Wielomian : Była, tyle że było dane pole powierzchni P walca i wyliczyć z tego maksymalny promień wysokość no i objetosc

Wielomian : Za 6 pkt banalny układ 3 rownan

Wielomian : Wykaz ze z dwoma wzorami skróconego mnożenia

Wielomian : Równanie z parametrem m, łatwe równanie trygonometryczne

Wielomian : Prawdopodobieństwo co koleżanka temat niżej napisała

House: ile wam wyszło w analitycznej równanie okręgu?

Dawid: a chyba 0.25 a b 5/12 ale nie pamietam

Policjant: x²+(u+1/3)²=coś tam

House: mi wyszło jak policjantowi

be:

	289
Mi wyszło r2 =
	9

be: A optymalizacyjne jakie miało być r? √6Pπ ?

Omikron: A kodowane z czego były?

be: Styczna do wykresu

be: A nie, jedno kodowane było. Nie pamiętam

be: Wiem ze mi wyszła 1/8

be: Juz pamiętam. Wielomian z niewiadomą a i podana reszta i ze się dzieli przez x−2

biodro: Ile Wam wyszedl parametr m?

Powała: nie przerobiłem ŻADNEGO zbioru i nie przygotowywałem się z maty i nie umiałem zrobić 3 zadań i to tych w środku arkusza, więc poziom był mega łatwy i sądzę, że będziecie mieć same setki to teraz wszyscy na politechniki pójdą

House: z kodowanego było, że wielomian jakiś W(x)=.. przy dzieleniu przez x−1 daje reszte 1 chyba

yht: 2π*r²+2π*r*h = P 2π*r*h = P−2π*r²

	P−2π*r2
h =
	2π*r

V = π*r²*h

	P−2π*r2
V = π*r2*
	2π*r

	P−2π*r2
V = r*
	2

	1
V =		* P*r − π*r3
	2

	1
V'(r) =		*P − 3π*r2
	2

	1
V'(r) = 0 ⇒		*P − 3π*r2 = 0
	2

−3π*r² = −0,5P

	−0,5P
r2 =
	−3π

	P
r2 =
	6π

r_m = √P/6π

	P   P−2π*   6π		2   P 3		P
hm =		=		=
	2π*√P/6π		2π*√P/6π		3π*√P/6π

	P		P
Vm = π*		*
	6π		3π*√P/6π

	P2
Vm =
	18π*√P/6π

Wojak: A ja liczyłem deltę w optymalizacji..

be: Według mnie zadania były albo bardzo łatwe (wykazywanie nierownosci, ciag, prawdopodobienstwo, otwarte) ale też te trudniejsze jak ostroslup czy też niestety dla mnie optymalizacja (teraz widzę, że banał, ale może będą ze 3 punkty)

tade: dla mnie matura średnia, niektóre zadania szły bez zastanowienia w kilku linijkach a niektórych niestety nie udało mi się zrobić, zabrakło miejsca i troche stres zadziałał niektóre zadania łatwizna niektóre trudniejsze − brakowało mi pośrednich

be: trygonometria również banalna bo wystarczyło wzor na cos2x a potem podstawić t

biodro: M mi wyszedl zbior pusty...

zef: Pamiętacie wynik z funkcji kwadratowej ? Mi wyszło m∊(−6,5;−5,5)\{−6}

tade: mi wyszło (−6;−5,5)

Alky: U mnie tak jak u Zefa

maniek: Jest gdzieś już arkusz?

yht: piłeczki: Ω = 8³ = 512 Zauważmy, że wśród kolejnych 8 liczb naturalnych jest: − dokładnie 2 które są podzielne przez 2 i niepodzielne przez 4 (liczby typu P₂) − dokładnie 2 które są podzielne przez 4 (liczby typu (P₄) − dokładnie 4 liczby nieparzyste (liczby typu N) Zdarzenia sprzyjające: P₄, N, N → 2*4*4*3 = 96 (mnożę razy 3 bo mam trzy warianty w ramach tego przypadku: (P₄, N, N), (N, P₄, N), (N, N, P₄) P₂, P₂, N → 2*2*4*3 = 48 P₄, P₂, N → 2*2*4*6 = 96 P₄, P₄, N → 2*2*4*3 = 48 P₂, P₂, P₂ → 2*2*2 = 8 P₄, P₂, P₂ → 2*2*2*3 = 24 P₄, P₄, P₂ → 2*2*2*3 = 24 P₄, P₄, P₄ → 2*2*2 = 8 A = 96+48+96+48+8+24+24+8 = 352

	A		352		11
P(A) =		=		=
	Ω		512		16

House:

	1		1
a styczna to y=		x−		ta
	2		2

tade: mi tak wyszlo

yht: zgadza się

Alky: rownanie z cosinusami ? 2/3π , π, 4/3 π ?

maniek: tak,

be: tak Z ciągami 2 ciągi wyszły? i w obu b=9?

zef: Tak

be: Ktoś zrobił kulą?

be: Ja tylko tyle, że srosunek wysokości małego do dużego to 2/3 Może 1 punkt będzie

martyna:

	√6
ja zrobiłam wyszło mi jakieś		tyle pominno ?
	6

lub: Też tak mam ^^

Jakub: Teraz moja kolej −> 4892

relaa: Wyznacz wszystkie wartości parametru m, dla których równanie 4x² − 6mx + (2m + 3)(m − 3) = 0 ma dwa różne rozwiązania rzeczywiste x₁ i x₂, przy czym x₁ < x₂, spełniające warunek (4x₁ − 4x₂ − 1)(4x₁ − 4x₂ + 1) < 0. Założenie Δ > 0 Δ = 36m² − 16(2m² − 3m − 9) = 4(m² + 12m + 36) = 4(m + 6)² 4(m + 6)² > 0 ⇒ m ≠ −6 (4x₁ − 4x₂ − 1)(4x₁ − 4x₂ + 1) < 0

	Δ
16(x1 − x2)2 − 1 < 0 [ (x1 − x2)2 =		]
	a2

	4(m + 6)2
16[		] − 1 < 0
	16

(2m + 12 + 1)(2m + 12 − 1) < 0

	13		11
(2m + 13)(2m + 11) < 0 ⇒ x ∊ (−		; −		)
	2		2

	13		11
Ostatecznie x ∊ (−		; −		) \ {−6}.
	2		2

maniek: Czy w zadaniu optymalizacyjnym trzeba było podać wysokość? Chyba o tym zapomniałem

khhhh: tak, trzeba było podać objętość, wysokość i promień

khhhh: mi się wydaję, że w tym roku jednak było trudniej niż w zeszłym – arkusz z 2016 robiłem kilka dni temu i przeleciałem przez niego jak strzała, a tutaj 3 godziny były w sam raz z drugiej strony może to być wina stresu, no i maturzyści zawsze mówią, że trudniejszy niż w zeszłym roku

maniek: Ja poległem na kuli, dowodzie z trójkątem i prawdopodobieństwem. No i nie zapisałem wysokości w ostatnim zadaniu. Reszta chyba dobrze

maniek: Ma ktoś już arkusz?

khhhh: jak wpiszesz w gugiel "Matura 2017: Matematyka [ROZSZERZENIE]" to znajdziesz

maniek: dzięki, mam

be: Dowód wam tak wyszedł? (xy − 2) + (x − y)² + (x − y)² > 0 ?

be: Do kwadratu ten pierwszy nawias

jc: Z podzielnością przez 4 proponuję od wszystkich możliwości odjąć przypadki, kiedy mamy wynik niepodzielny przez 4. 8³ − 4³ − 3*2*4² = 352 wszystko − iloczyn 3 nieparzystych − iloczyn 2 nieparzystych i 2 lub 6 (2 lub 6 mozemy postawić na 3 sposoby)

prsa: be, wolfram pokazuje ze Twoj wynik po przemnozeniu daje takie same liczby jak w danych Czyli jestli przy (xy−2)² −> dales kwadrat to jest OK

khhhh: be, też tak dowód wyszedł, no i jeszcze napisać, że (x−y)² zawsze będzie większe od zera dla x≠y

be: Tak dałem I jeszcze odpowiedni komentarz, bo nie było tam znaku ≥. Bez komentarza by się mofli przyczepić

prsa: A jakie mialby wyjsc liczby w ciagu art. i geom? pamieta moze ktos tylko b=9 mi sie cos przypomina

be: pierwszy ciag 5 9 13 drugi coś z ulamkami przy czym b również 9

be: A dowód w planimetri jak zrobiliscie?

I'm afraid:

	1		1
drugi chyba a=15		b=9 c=2		chyba
	2		2

khhhh: a=2,5, b=9, c=15,5 albo a=5, b=9, c=13

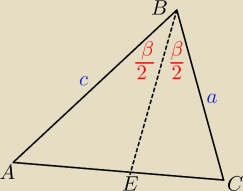
yht: P_ABE + P_BEC = P_ABC

1		1		1
	c*BE*sin(β/2) +		a*BE*sin(β/2) =		a*c*sinβ
2		2		2

β/2 = α

1		1		1
	c*BE*sinα +		a*BE*sinα =		a*c*sin(2α) |*2
2		2		2

c*BE*sinα + a*BE*sinα = a*c*sin(2α) c*BE*sinα + a*BE*sinα = 2a*c*sinα*cosα |:sinα c*BE + a*BE = 2a*c*cosα BE(a+c) = 2a*c*cosα |:(a+c)

	2a*c*cosα
BE =
	a+c

	2a*c*cos(β/2)
BE =
	a+c

ale siedząc w sali raczej bym tego nie wymyślił

khhhh: ten pierwszy ciąg odwrotnie, czyli tak jak napisał I'm afraid

Rafal: Co do planimetrii: twierdzenie o dwusiecznej +2 x twierdzenie cosinusów.

khhhh: http://plikicke.cie.men.gov.pl/_EGZAMIN_MATURALNY/2017/FORMULA_OD_2015/matematyka/MMA-R1_1P-172.pdf tutaj oficjalnie zadania

Adamm: a=2,5, b=9, c=15,5 ale a−2, b, 2c+1 nie jest geometryczny jeśli chodzi o mnie, przeczytałem że iloczyn ma być równy 4, więc... i nie zabrałem −6 od nierówności

Wojaj: Schematyczna była ta matura. Wg mnie do stracenia były punkty tylko z tej kuli, moze z prawdopodobieństwa Pierwsze 8 zadań zrobilem w 20 minut

Wojaj: Jest geometryczny Adamm

Adamm: 0,5, 9, 32 ? nie jest geometryczny

Wojaj: Faktycznie, sorry. No to pułapkę zrobili. Ale to chyba 1 punkt?

Adamm: właśnie, szkoda że pułapkę zauważyłem, ale samemu sobie kłody pod nogi kładę...

be: A ogółem jak Ci poszło Adamm

Adamm: wszystko zrobiłem, chyba dobrze koło 90 myślę że będzie

Dawid: A w tym zadaniu zamkniętym z kątem wpisanym to 52,5 ?

Adamm: tak

be: Tak. Miałes tam dwa trojkaty charakterystyczne Kat w środku to 60 + 45 A alfa był połowa

be: To gratuluję Adamm

Dawid: Adam, a jak Ci wyszło w wyznaczeniu równania okręgu? Co tam trzeba było w ogóle zrobić? Ja podmieniłem środek do tej prostej, czyli S(x, rownanie prostej) potem do za a i b do rownania okregu i 2 punkty podstawilem, czyli wyszly mi 2 rownania z 2 niewiadomymi, a oraz r nie wiem czy mam to dobrze

Dawid: Jeszcze w tym ostatnim zadaniu się pogubiłem i nawet nie zdawałem sobie sprawy, że dadzą tak niejasne zadanie z liczbą "P" ... Dopiero po wyjściu mnie oświeciło, że wynik też mógł wyjść r+p ileś tam, eh

Adamm: (x−x₀)²+(y−y₀)²=r² podstawiasz 2 punkty, odejmujesz i dostajesz funkcję liniową i potem z punktu przecięcia tych dwóch prostych dostajesz x₀, y₀ r można było ostatnie policzyć

be: A w ogóle jak miało wyjść?

	1		189
U mnie x2 + (y −		)2 =		Ale chyba coś źle promien
	3		9

Adamm: 289/9

Dawid: Pamiętasz ile wyszła pierwsza współrzędna środka?

Adamm: to co be pisze, tylko promień ten co podałem

relaa: Zadanie z ciągiem a = 5 ∧ b = 9 ∧ c = 13 lub

	31		5
a =		∧ b = 9 ∧ c =		.
	2		2

Dawid: Średniawka ta maturka mi poszła, jutro liczę na 70% z informatyki, ostatnia szansa @_@

be: Adamm, czyli dobrze mi wyszło. Pomyłka nie 189 tylko 289

Metis: No to dostaliście piękny prezent od CKE Zadania według mnie przynajmniej pod względem obliczeń nieporównywalne do matury z 2016. Pierwsze 7 zadań to darmowe punkty. Podobnie dwa ostatnie − schemat i rozwiązanie kilku układów, za ogromną ilość punktów.

jc: Metis, w danym roku to ma niewielkie znaczenie.

Metis: Masz racje jc czekam na statystyki

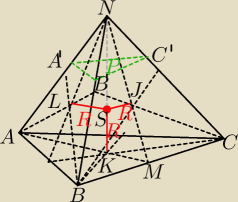
yht: Zadanie z kulą: a = 6 LS = SJ = SK = R NK = h NS = h−R

	1		a*√3
KM =		*		= √3
	3		2

	a*√3
NM =		= 3√3
	2

z pitagorasa w ΔNKM: NK² + KM² = NM² H² + KM² = NM² H² + 3 = 27 H² = 24 H = 2√6

	2		a*√3
NJ =		*		= 2√3
	3		2

z pitagorasa w ΔNSJ: SJ² + NJ² = NS² R² + 12 = (2√6−R)² R² + 12 = 24 − 4√6R + R² 4√6R = 12

	√6
R =
	2

Vm		8		2
	=		= (		)3
Vs		27		3

	8
Ostrosłup A'B'C'N jest podobny do ostrosłupa ABCN i k3 =
	27

	2
stąd k =
	3

NP		2
	=
NK		3

NP		2
	=
2√6		3

	4√6
NP =
	3

SN = NK − KS SN = H − R

	√6
SN = 2√6 −
	2

	3√6
SN =
	2

SP = SN − NP

	3√6		4√6		9√6		8√6		√6
SP =		−		=		−		=
	2		3		6		6		6

Wojak: Za dojście do NJ=2√3 będzie punkt?

be: Adamm, w ciągach chyba nie trzeba było jednak odrzucać tego jednego, oba są poprawne

Marcin: Za najprostsze uważam zadanie z ciągami, równanie okręgu też nietrudne (choć chyba popełnilem błąd obliczeniowy), równanie trygonometryczne to też był banał. Za najtrudniejsze uważam zadanie z kulą w ostrosłupie, ostatnie zadanie z pochodną (przez to że pole było niewiadomą ze stresu było strasznie ciężko wszystko dobrze policzyć) i osobiście typuję też prawdopodobieństwo − schematycznie łatwe, ale mnóstwo opcji do wzięcia pod uwagę.

Mila: Zadanie z czworościanem:

	2
k=		− skala podobieństwa ostrosłupów
	3

H− wysokość danego czworościanu o krawędzi a=6

	1
R=		H − promień kuli wpisanej
	4

h− wysokość czworościanu odciętego

	2
h=		H
	3

d− odległość środka kuli od płaszczyzny π R+d+h=H

1		2
	H+d+		H=H
4		3

	1
d=		H
	12

	a√6
H=		=2√6
	3

	1
d=		*2√6
	12

	√6
d=
	6

======

khhhh: co

Marcin: Przy czworościanie zrobiłem do momentu, w którym musiałem obliczyć promień okręgu − skąd wiadomo, że wynosi 1/4H? Resztę mam policzoną, tylko brakuje promienia i roozwiązania do końca

typek: czy jeśli usuwałem niewymierności z mianownika w zadaniu optymalizacyjnym to stracę punkty? w sumie wynik ten sam, tylko troszeczkę inaczej zapisany

tyokke: Mam pytanie, w zadaniu maturalnym z czworoscianem, policzylem cale zadanie, tylko zamiast skali podobienstwa ostroslupow napisac 2/3, to napisalem 1/3, ile punktow moge miec za to uciete skoro zadanie jest za 4 punkty, a mi zamiast √6 wyszło 5√6 6 6

be: Właśnie, skąd to 1/4 H?

I'm afraid: tyokke około 2−3 pkt

tyokke: @I'm afraid, ale uciete, czy tyle dostane?

bhi: Jaki wynik wyszedł w równaniu trygonometrycznym? Były 2 opcje i cosx=−1 dla π, a druga sprzeczna?

Mila: Dla Marcina Czworościan foremny− ciekawa bryłka i warto znać jej własności. https://pl.wikipedia.org/wiki/Czworo%C5%9Bcian_foremny

be:

	1
bhi druga była −
	2

Omikron: Makler coś nie pisze, mam nadzieję że mu dobrze poszło

PrzyszlyMakler: Dziękuję, że się martwisz. Musiałem ochłonąć.

PrzyszlyMakler: x²y²+2x²+2y²−8xy+4 > 0 (xy−2)² + 2(x−y)² > 0 bla bla komentarze, dobrze zrobione przekształcenia?

Ajtek: Rozszerzenie na kolana nie powaliło.

Emilia: dla mnie najgorsze były te zadania na uzasadnienie z tym trójkątem robiłam za pomocą twierdenia cos a potem parze w odpowiedziech i to można było zrobić korzystając ze wzroru na pole trójkąta−teraz mi się to wydaje łatwe jak nie wiem co ale trzeba było wpaść na taki pomysł

Emilia: oczywiście nie udało mi się tego zrobić z twierdzenia cos

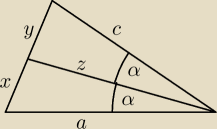
khhhh: z twierdzenia cosinusów też można było bo ja tak zrobiłem tw. o dwusiecznej:

x		a
	=
y		c

x²=a²+z²−2az*cosα y²=c²+z²−2cz*cosα

x2		a2+z2−2az*cosα
	=
y2		c2+z2−2cz*cosα

a²(c²+z²−2cz*cosα)=c²(a²+z²−2az*cosα) a²c²+a²z²−2a²cz*cosα=c²a²+c²z²−2ac²z*cosα z²(a²−c²)=2acz(a−c)cosα z²(a−c)(a+c)=2acz(a−c)cosα

	2ac*cosα
z=
	a+c

potem zorientowałem się, że żeby podzielić przez (a−c) trzeba założyć, że a≠c, więc obliczyłem jeszcze z dla przypadku, gdy a=c (jest to wtedy wysokość trójkąta równoramiennego, więc jest to banalne) wiem, że przekombinowane, ale coś takiego wymyśliłem, a nie miałem czasu żeby zastanawiać się nad ładniejszym rozwiązaniem

Emilia: dosyć kiepsko napisałam tą maturę a jestem dobra z matematyki

tyokke: Moim zdaniem matura na poziomie, zrobilem wszystkie zadania, niedokonczylem tego dowodu geometrycznego, zle zrobilem kombinatoryke, no i bledy rachunkowe, myslalem ze bede mial ponad 90%, teraz liczę na 70% ze względu na te błędy...

mat: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=4900 wpis Ety

Wojak: Matematyka podstawowa na 100 i rozszerzona na 50 to tak naprawdę na większosc kierunkow się dostaniecie

PrzyszlyMakler: Zerkniecie 16:53?

khhhh: tak, dobrze, zresztą masz te zadanie zrobione tutaj https://matematykaszkolna.pl/strona/4892.html

mikler: Makler

PrzyszlyMakler: nie patrzyłem @khhhhh a na interii gościu zrobił inaczej ode mnie, ale dizęki, już wiem.

relaa: Zależy też jaki komentarz dałeś.

Maryla27: Zadanie 11 Piłeczkę losujemy "z pudełka" i zwracamy "do urny". ?

khhhh: jakby nie patrzeć urna może być pudełkiem

Maryla27: ...albo innym pojemnikiem i wtedy bez zwracania.

Omikron: Makler, a jak ogólnie oceniasz?

PrzyszlyMakler: Moim zdaniem trudniejsza niż rok temu. Jak robiłem zeszłoroczną w tym roku (około miesiąc temu) to nie umiałem jedynie zadania z analitycznej. W tej prawdopdoboieństwo mi się nie podobało [nie wpadłem na przeciwne], stereometria (zeszloroczną stereo zrobiłem) no i planimetria, ale planimetria była łatwa, zapisałem tw. o stycznej i dwa tw. cosinusów, ale zamiast podzlić, to odejmowałem. Poprawić− poprawiłem. Dostać się− dostanę. Ale czuję taki niewyobrażalny zawód. Prawdopddobnie przystapię jeszcze raz za rok dla ambicji.

Adamm: PrzyszlyMakler, nie ma sensu tracić głowę dla ambicji będziesz tracił tylko swój cenny czas dla takich głupot

PrzyszlyMakler: @Adamm, nie mam zamiaru się przygotowywać, bo materiał mam naprawdę porzadnie opanowany. Pójdę "na żywioł" i mam nadzieję, że będzie lepiej. Przerobiłem wszystkie arkusze z ostatnich 4 lat ze wsztystkich wydawnictw, próbne, czerwcowe, majowe, techników, i na palcach jednej ręki policzyłbym wyniki poniżej 80, a tutaj zawód, bo zepsułem zadanie z okręgiem, bo przeczytałem, że te punkty są styczne... także liczę je sobie na 0. I wynik to będzie coś ok. 70%.

Adamm: PrzyszlyMakler, ja nawet tego nie sprawdzałem, a skończyłem przed czasem trochę szkoda, bo popełniłem parę tragicznych błędów, ale życia mi to nie zmieni myślę że ty powinieneś myśleć tak samo

Księżna Łucja: Dzisiaj zadania były albo bardzo proste albo dość skomplikowane. Ciągi,trygonometria,równanie okręgu chyba najłatwiejsze punkty i to w sporej ilości. Ale zadanko bodajże kula wpisana w czworościan to jedna wielka ściana(piszę z perspektywy osoby która nie miała rozszerzenia w szkole)

PrzyszlyMakler: też tak uważam. Były 4 zadania bardzo łatwe i ze 4 znacznie trudniejsze. Ale cóż, było minęło. Ten okrąg to ubolewać będe do przyszłego roku albo dłużej, ale cóż. Ważne, że się udało, na przekór całemu światu, bym rok temu poszedł na "cokolwiek" na studia.

Omikron: A po SGH perspektywy duże, także tak czy inaczej gratuluję. Jakbyś miał jakieś pytania dotyczące SGH to pisz

be: Makler a na ile napisałeś podstawę?

Martin: Głupie błędy i zostałam z wynikiem w okolicach 70%... Łatwiej będzie mi resztę na kasie liczyć

PrzyszlyMakler: Omikron A skąd Ty masz informacje o SGH? Jak masz gg to napisz 45554187

PrzyszlyMakler: Podstawa 100

Omikron: Studiuję na SGH

Metis: Mamy podobne podejście do takich spraw Adammm

PrzyszlyMakler: Omikron, napiszesz na gg? Pewnie że mam pytania

Wojak: Ale chodzą słuchy, że matura była trudna. Wiadomo, że od osób, które siedzą na forum matematycznym się tego nie usłyszy. Ale jeśli rzeczywiscie dla wielu osób trudna, to może będą niskie wyniki. Liczy się przecież porównanie do ogółu

Omikron: Napiszę jak do domu wrócę

Adamm: porównując to z maturą próbną Pazdro z którą miałem styczność, to była ona strasznie łatwa (może to nie było Pazdro, w sumie nie pamiętam)

PrzyszlyMakler: Ok. Dziękuję, że zaoferowałeś

Omikron: Wojak, co roku ogół maturzystów mówi że trudna, więc tak raczej wniosków co do progów się nie wyciągnie.

Jasiek2234: Poziom trudności widać dopiero na wykresach wyników, które udostępnia cke.

Wojak: Czyli dopiero lipiec. Ehh ciężko będzie tyle wytrzymać

Marcin : Wg mnie była trudniejsza niż rok temu i to o dużo pozdrawiam

AiO: A swistak mowi niemożliwe

Behemot: Czytałem dzisiaj jakiś tam artykulik, nawet nie wiem gdzie, w którym wypowiadał się jakiś profesor na temat tegorocznej matury. Powiedział coś w stylu, że ludzie którzy mają 80%+ powinni sobie w miare przyzwoicie poradzić na studiach. To ja chyba sobie pozamiatam podłogi.

Mila: A ile masz kotku?

Behemot: Coś koło 70, ale raczej troszkę mniej. Zwaliłem zadanie z parametrem i pewnie będzie za nie 0 punktów, znając sposób, w jaki tego typu zadania oceniają. Nie dałem założenia x₁<x₂ czy coś takiego.

Mila: Pouczysz się w wakacje i dasz radę. Na pewno dostaniesz się tam , gdzie chcesz, 70% to dobry wynik.

Behemot: Ta, pouczę się w wakacje...

Behemot: Nie narzekam na te procenty, fizykę jeszcze jakoś napiszę i powinno być dobrze.

Marcin : Mila a Ty ile będziesz miała ?

Metis: 100 %

.......:

	P		√P
czy jak napisałem w ostatnim √		=		=r jest poprawne
	6π		√6π

TakieFajne: Jasne

.......: dzięki

behroror: Ta matura jest bardzo prosta w porównaniu z maturą z ubiegłego roku. Tak jak ktoś pisał wyżej : "prezent od ...". Moim zdaniem łatwo było uzyskać min. 90% z tegorocznej matury. Chemia i biologia również była BANALNA.

Kaga: Przecież chemii i biologii nie pisano jeszcze

PrzyszlyMakler: Kaga, nie karm trolla

behroror: Tzn. ja pisalem swoją kilka lat temu. Ktoś mi pokazywal arkusz dzień temu , a to był pewnie z tamtego roku. Sorki xd. Nie jestem na bieżąco i zapomniałem kiedy są matury.

Kaga: Spoko Ogólnie to trudność to pojęcie względne i ciężko powiedzieć co kiedy jest trudniejsze Dla ludzi z matematyka pisz wszystko jest łatwe, ale tak to jest

Alky: behroror tak jak Kaga pisze "trudność to pojęcie względne". Według mnie na przykład matura z ubiegłego roku była bardzo łatwa i tylko 1 zadanie sprawiło mi problem. To był bodajże jakiś dowód z planimetrii. Ta jak na moje była w porównaniu do ubiegłorocznej cięższa.

Alky: Choć i ta ta jakoś specjalnie trudna nie była, a zadanie z optymalizacji było generalnie jednym z łatwiejszym jakie widziałem ( jeśli chodzi o te maturalne). Wszsytko podane, tylko trzeba sięna literkach pobawić. To chyba miało być tą trudnością. Tak czy inaczej i tak jestem specjalny i się gdzieś na początku pomyliłem, potem wszsytko skreśliłem i zacząłem liczyć od nowa, ale brakło mi czasu więc nawet z tego −5 lub −6 pkt ... ALE BAWIŁEM SIĘ SZAMPAŃSKO

Omikron: Ja uważam, że poziom podobny do ubiegłorocznego rozszerzenia, więc jak widać każdy ma inną opinię

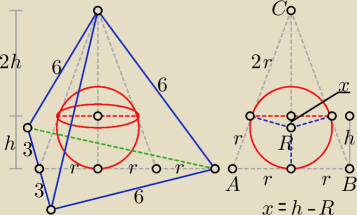
Bogdan: Proponuję takie rozwiązanie zadania z czworościanem (oznaczenia jak na rysunku), to jest szkic rozwiązania, pominąłem komentarze i wyjaśnienia.

	1
Skala podobieństwa k = 3√8/27 = 2/3, r =		*6√3 = √3
	6

	2√6
3h = √ 9r2 − r2 = √ 27 − 3 = 2√6, h =
	3

	8r		√6
Pole trójkąta ABC: PΔ = 3h*r = 2√6*√3 i PΔ =		*R = 4√3*R ⇒ R =
	2		2

	2√6		√6		√6
x = h − R =		−		=
	3		2		6

AiO: dziekuje Bogdan Ladne rozwiazanie . Sie przyda do matury .

Rafal: Co do zadania z czworościanem: można też było sobie przypomnieć, że środek kuli wpisanej leży na przecięciu wysokości, a te przecinają się w stosunku 3:1. Płaszczyzna π dzieli jedną z wysokości na odcinki w stosunku 2:1. Wystarczy więc jedynie policzyć długość tej wysokości i poodejmować długości odpowiednich odcinków.

Mila:

.-): matura była w miarę prosta ale i tak obleje ją tyle ile statystycznie oblewa