równanie z jedna niewiadoma ejsi1: Rozwiąż równanie: x³−3x+1=0

kochanus_niepospolitus: sprawdź jeszcze raz czy aby na pewno tak wygląda to równanie

ejsi1: tak

kochanus_niepospolitus: to na poziomie liceum, a i nawet studiów tego nie rozwiążesz

ejsi1: ok, to wtedy podam te przybliżone wartości, które mi podaje komputer

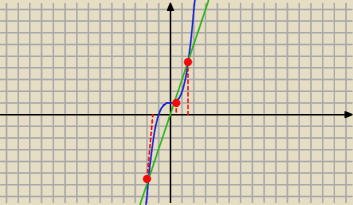mati: g(x)=x³+1 h(x)=3x Równanie ma trzy rozwiązania

Adam: 2cos(2π/9), 2cos(8π/9), 2cos(14π/9)

Adam: myślę że miło jest wiedzieć na co patrzysz

Mariusz: kochanus jak porówna wielomian z dwumianem Newtona to dostanie układ równań który przekształci we wzory Vieta dla trójmianu kwadratowego Jeżeli trójmian kwadratowy będzie miał ujemny wyróżnik to wtedy gdyby chciał rozwiązywać metodą algebraiczną musiałby wejść w zespolone ale można zrezygnować z metody algebraicznej i skorzystać z trygonometrii Kochanus nie przesadzaj zdaje się że nawet w zbiorze Krysickiego i Włodarskiego jest szkic rozwiązania

Mila: x³−3x+1=0

	−3		1		1		3
Δ=(		)3+(		)2=−1+		=−		<0 równanie ma 3 rozwiązania rzeczywiste.
	3		2		4		4

	α+2kπ
xk+1=2√−(−3)/3*cos		, k∊{0,1,2}
	3

	α		3		1		2π
x1=2cos		i cosα=		, ⇔cosα=−		⇔α=
	3		−6		2		3

	2π
x1=2cos
	9

	8π
x2=2*cos
	9

	14π
x3=2*cos
	9

możesz sprawdzić w wolframie, czy te liczby spełniają równanie.