ostrosłup Ala: Podstawą ostrosłupa jest trójkąt równoramienny o podstawie a i kącie przy podstawie 60. Wszystkie krawędzie boczne tworzą z wysokością ostrosłupa kąt 60. Oblicz promień kuli opisanej na tym ostrosłupie.

Ala: Ktoś pomoze?

Adamm: podstawa jest trójkątem równobocznym

	2   h 3
tg60o=
	H

h=a√3/2 H=a/3 P_p=a²√3/4

	1
V=		*[a2√3/4]*a/3 = a3√3/48
	3

Ala: A jak policzyć promień tej kuli?

Adamm: sorry, V=a³√3/36

Ala: A czemu trzeba liczyc objetość?

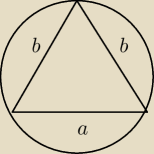
Adamm: ah, no tak zapędziłem się, znowu

	2h/3
sin60o=
	b

b=2a/3

	abc		abc
P=		⇒ R=
	4R		4P

ze wzoru Herona P=5a²√21/36

	4a√21
R=
	105a2

Adamm: sprawdź czy dobrze policzyłem P oraz R, liczyłem na szybko

Ala: A można by było obliczyć go z twierdzenia piagorasa

	2		a√3
R2=(H−R)2+(				)2
	3		2

Adamm: tak

Mila:

	2
R=		a ?
	3

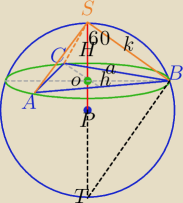
Mila: a− dł. boku Δrównobocznego ABC W ΔSOB:

	2   h 3
tg60=
	H

	2√3h
H=
	9

	2√3		a√3
H=		*
	9		2

	a
H=
	3

	2a
k=
	3

ΔSBT− trójkąt prostokątny

	k
cos60=		, |ST|=2R
	|ST|

1		2a   3
	=
2		2R

	2
R=		a
	3

===========