Liczby zespolone M.: Wiem, że to nie ta podstrona, ale nie wiem (znaczy wiem, ale nie wiem, czy dobrze rozumuję), mianowicie: 1) Na płaszczyźnie zespolonej zaznacz zbiór: |z+2|=|z−7|.

M.: W sensie, nie wiem, jak wejść na podstronę studencką, to rozumowanie (nie wiadomo, czy błędne), dotyczyło zadania. Się zapętliłam.

AiO: Masz po lewo nawigacje i tam dla studenta

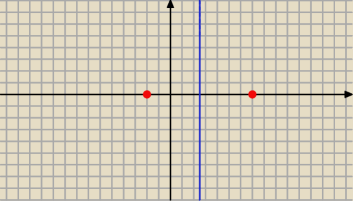
Adamm: |z+2|=|z−7| to punkty równo odległe od −2 jak od 7

M.: Ok. Czy mogę to rozpisywać podobnie jak dla wartości bezwzględnej czy jest to stricte zabronione?

Adamm: zależy co masz na myśli |z+2|=|z−7| z+2=z−7 lub z+2=7−z ? no tak to nie możesz co najwyżej podstawić z=x+yi ale sposób w jaki ja to zrobiłem jest najprostszy i najszybszy

M.: Ok, zrobiłam tak ostatnio i równocześnie narysowałam tę oś pionową i mi nie zaliczył; tzn., że jak cały ten "z" jest ujemny ze strony lewej, a z prawej jest dodatny, to jest to sprzeczność, ale nie zaliczone miałam całości pewnie za te bezwzględne. No cóż, zdarza się.

Adamm: w sensie 21:33? jak sama widzisz z rysunku, rozwiązań jest nieskończenie wiele

M.: Tak, w sensie 21:33

Mila: z=x+iy, x,y∊R Interpretacja geometryczna równania: |z+2|=|z−7| |z−(−2)|=|z−7| symetralna odcinka o końcach : (−2,0) i (7,0)

	5
Re(z)=
	2

	5
albo x=		,
	2

M.: z=2,5 jest bardzo źle? Skoro to oznacza tyle samo, co x=2,5; y=0?

M.: yi, niedociśnięcie klawisza.

M.: Pardon, yi w takim wypadku należą do zbioru liczb rzeczywistych,

Mila: z=2,5 może być, patrz jednak na zapisy z ćwiczeń.