Krawedzie Bryly: Czy ostroslup moze miec 30 scian bocznych i 50 krawedzi? Jak uzasadnic odpowiedz?

Kaspian: w−k+s=2 w−20=2 w=22 czyli podstawa musi miec 21 wierzchołków 21 krawedi podstawy + 21 krawedzi scian =42 krawedzie nie moze istniec To tak na szybko pewny nie jestem

Kaspian: a sciany boczne

Kaspian: 30 ścian bocznych ma ostrosłup o 30 krawędziach podstawy i 31 wierzchołkach nie może mieć 50 krawędzi

Adamm: jeśli ma 30 ścian bocznych to jego podstawa jest 30kątem, a wtedy ma 60 krawędzi

Kaspian: mozna tez z twierdzenia eulera tak jak pisałem tylko w=21

Mila: II sposób n−kąt w podstawie 2n−liczba krawędzi n+1 − liczba ścian −−−−−−−−−−− n=30 w podstawie 30−kąt 2*30=60 liczba krawędzi sprzeczność: 60≠50 Nie istnieje.

Bryly: Czy w ostroslupie krawedzi bocznych jest tyle samo co scian bocznych?

Adamm: tak

Bryly: 2) 40 krawedzi bocznych i 20 scian Wydaje mi się, ze nie, ale dlaczego?

Bryly: 2) Czyli majac 40 krawedzi bocznych mialby juz 40 scian bocznych dobrze? 3) 11 scian i 20 krawedzi? Tak, bo 1 sciana to podstawa a 10 scian to sciany boczne zatem w podstawie 10−kat, czyli razem 20 krawedzi. 4) liczba krawedzi w ostroslupie musi byc parzysta bo krawedzi podstawy jest tyle samo co krawedzi bocznych dobrze?

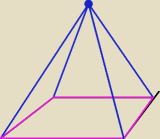
Mila: n=4− liczba boków w podstawie ( kątów) k=2*4=8 − liczba krawędzi s=4+1 − liczba ścian ( 4 boczne i podstawa) w=4+1− liczba wierzchołków −−−−−−−− 40 krawędzi bocznych to 40 ścian bocznych

Bryly: a 3) i 4) ok?

Mila: Dobrze. Narysuj sobie jakiś ostrosłup, a potem uogólniaj.