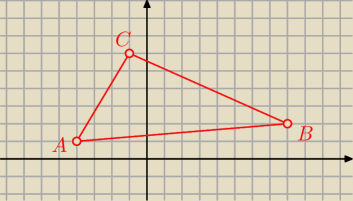
Punkty A(-4,1) b(8,2) c(-1,6) są wierzchołkami trójkąta abc
jolaaaaa: Punkty A(−4,1) b(8,2) c(−1,6) są wierzchołkami trójkąta abc
napisz rownanie prostej zawierającej
a) wysokość tego trójkąta poprowadzoną z wierzchołka B
b) srodkową tego trójkata poprowadzona z wierzcholka b
8 maj 15:26
Jerzy:
I z czym masz problem ?
8 maj 15:27
jolaaaaa: jakbym nie miala problemu to bym nie pisala
8 maj 15:32
Jerzy:
Poczytaj jak napisać równanie prostej mając dwa jej punkty.
8 maj 15:35
po prostu Michał:
a)
1) poprowadz prosta symetralna do AC przechodzaca przez wierzcholek B
8 maj 15:35
Jerzy:
Nie symetralną, tylko prostopadłą !
8 maj 15:39
po prostu Michał: tak tak, pardoncik, mialem na mysli prostopadla oczywiscie

8 maj 15:41
jolaaaaa: :(
8 maj 15:43
po prostu Michał: co jest jola?
8 maj 15:44
po prostu Michał: jola lojalna lojalna jola
8 maj 16:00
po prostu Michał:
a)
| | YC − YA | |
prosta AC ma wspolczynnik kierunkowy aAC = |
| : |
| | XC − XA | |
prosta do niej prostopadla ma wspolczynnik kierunkowy
| | 3 | | 5 | |
a = − |
| (proste sa prostopadle gdy a1*a2 = −1, zatem |
| *x = −1 itd) |
| | 5 | | 3 | |
no i teraz ta prostopadla musi przechodzic przez B, wiec podstawiamy
wspolrzedne B do wzorku y = ax + b (bo to rownanie prostej)
| | 3 | |
2 = − |
| * 8 + b −−> b = ... |
| | 5 | |
| | −3 | |
albo mozna szybciej, wiemy ze a = |
| , oraz B(8,2) |
| | 5 | |
| | 3 | |
zatem y = − |
| (x−8)+2 = ... |
| | 5 | |
(tutaj skorzystalem z tego, ze y = a(x−x
1)+y
1) gdzie (x
1,y
1) to wspolrzedne jakiegos punktu
nalezacego do tej prostej
8 maj 16:07
po prostu Michał:
b(8,2)
b) w tym wypadku musimy znalezc srodek odcinka AC no i potem co,
prosta przechodzaca przez srodek i przez wierzcholek B(8,2)
| | −4−1 | | 1+6 | | 5 | | 7 | |
SAC = ( |
| , |
| = (− |
| , |
| ) |
| | 2 | | 2 | | 2 | | 2 | |
skoro prosta ma przechodzic przez B i S to :
| | 3 | |
y = − |
| (x − 8) + 2 = ... |
| | 21 | |
8 maj 16:54

 b(8,2)
b) w tym wypadku musimy znalezc srodek odcinka AC no i potem co,
prosta przechodzaca przez srodek i przez wierzcholek B(8,2)
b(8,2)
b) w tym wypadku musimy znalezc srodek odcinka AC no i potem co,
prosta przechodzaca przez srodek i przez wierzcholek B(8,2)