dowod przyszłymakler:

	1
Udowodnij, że jesli a∊ (0;1) b∊ (0;1) oraz log1/3a*log1/3b = 4 to a*b≤
	81

1
	x = a
3

1
	y = b
3

x*y=4

	4
x=
	y

	1		1
a*b=		x+y =		(4+y2)/y y≠0
	3		3

	4+y2
Teraz udowodnię, że funkcja f(y) =		przyjmuje wartości większe równe 4.
	y

	2y(y)−(4+y2)		(y−2)(y+2)
f'(y)=		=
	y2		y2

	4+4
fmax = f(−2) =		= −4
	−2

	4+4
fmin= f(2) =		= 4
	2

1. nie wiem dlaczego wyszło mi fmax < fmin 2. no, nie udało się udowodnić... ktoś mógłby pomóc tym sposobem?

kochanus_niepospolitus: emmm ... a jak wyznaczyłeś które ekstremum jest które?

kochanus_niepospolitus: po drugie ... masz udowodnić, że f(y) ≤ 4 dla ∀_y∊Df

kochanus_niepospolitus: tfu (to ostatnie )

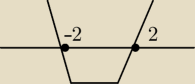
przyszłymakler: (y−2)(y+2) = 0 f(−2) = max f(2) = min na rysunku graf pochodnej

przyszłymakler: ale dziedziną y jest chyba y ∊R − {0}

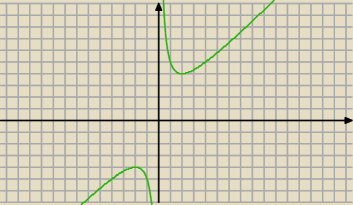
Jerzy: Tutaj masz wykres: f(y)

kochanus_niepospolitus: no i wszystko cacy Ci wyszło zauważ, że funkcja f(y) NIE JEST funkcją ciągłą

	4
f(y) = y +		... ten drugi człon powinien Cię naprowadzić na to jak to mniej więcej
	y

będzie wyglądała ta funkcja

przyszłymakler: Ok, ale dla y<0 funkcja przyjmuje wartości mniejsze od −4, więc to nie udowadnia tezy

Jerzy: A dlaczego nie ?

Jerzy: A nie ....

kochanus_niepospolitus: no ale przecież, dla y<0 zachodzi: y<0 i x<0 ... a więc a,b > 1

kochanus_niepospolitus: a mamy dane, że a,b ∊ (0,1) (czyli x,y >0)

przyszłymakler: No tak, dziękuję! Wszystko rozumiem

relaa: Może w ten sposób? Wychodząc od prawdziwej nierówności dla a, b ∊ (0 ; 1) [√log_¹/3(a) − √log_¹/3(b)]² ≥ 0 log_¹/3(a) + log_¹/3(b) = log_¹/3(ab) ≥ 2 • √log_¹/3(a) • log_¹/3(b) = 2 • 2 = 4

	1		1
ab ≤ (		)4 =		.
	3		81