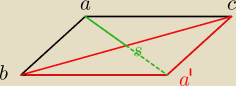
Planimetria, dowód Ith: Witam, mam drobny problem ze zrozumieniem rozwiązania tego zadania: "Odcinek AS jest środkową trójkąta ABC. Udowodnij, że |AB |+ |AC | > 2|AS|" rozwiązanie: Otrzymany czworokąt ′ ABA C jest równoległobokiem (bo ′ A C = AB i A ′B = AC ), którego przekątne przecinają się w punkcie S (bo S jest środkiem przekątnej BC ). W takim razie 2AS = AA ′ < AB + BA ′ = AB + AC . Będę wdzięczna jeśli ktoś wyjaśni co tu się wydarzyło, a przede wszystkim dlaczego.

Ith: Cofam, właśnie zaskoczyło

Astaroth : Masz trójkąt aba' i w nim suma dwóch boków musi być większa od długości trzeciego czyli twojego aa'