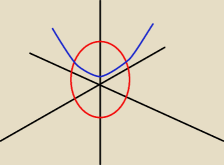
objętość bryły Beorn: Obliczyć objętość bryły ograniczonej powierzchniami: z=√25−(x²+y²) z=1+√x²+y² Zrobiłem sobie taki rysunek poglądowy ale nie wiem jak się za to dalej zabrać i czy w ogóle go dobrze zrobiłem (Wiem że na rysunku powinna być tylko górna połowa kuli) Myślałem o tym czy nie powinienem przyrównać tego √25−(x²+y²)=1+√x²+y² i potem podzielić to na 2 obszary całkowania ale ciężko mi sobie to wyobrazić

jc: x² + y² + z² = 25, z≥0, górna połowa sfery x²+y² = (z−1)², z≥1, stożek skierowany dzióbkiem w dół powierzchnie przecinają się na wysokości z=4. z² + (z−1)² = 25, z≥1. Masz więc coś w rodzaju rożka z lodami.

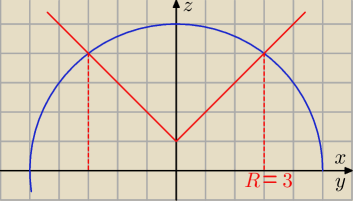
g: To będzie część wspólna kuli i stożka. Przecinają się na okręgu o promieniu R=3. Całkę łatwiej liczyć we współrzędnych cylindrycznych. V = ∫₀^2πdα ∫₀^R[√25−r² − (1+r)] r dr = 2π ∫₀^R[√25−r² − (1+r)] r dr

Beorn: Wiedząc że z=4 podstawiłem go pod równanie kuli przy którym przyjmuje że y=0 więc wychodzi mi przedział całkowania dla x od 3 do −3 .Teraz muszę skleić 2 całki w których jedna będzie miała granicę ze wzoru na kule a druga ze wzoru na stożek?

Beorn: cylindrycznych chyba jeszcze nie miałem tylko biegunowe

Beorn: czy to jest dobrze ? −3≤x≤3 1+x≤y≤√25−x²

g: x ∊ [−3; 3], y ∊ [−√3²−x²; √3²−x²]