Płaszczyzna zespolona Dominika: Witajcie, proszę Was o pomoc w następującym zadaniu: mam narysować Zbiór M1 = { z: |z| + Im(z) ≤ 2 } na płaszczyźnie zespolonej. Doszłam do czegoś takiego: z= x + yi, moduł |z| = √x² + y² i Im(z) = y podstawiłam do wzoru z zadania: √x² + y² + y ≤ 2 / (...)² (√x² + y² + y)² ≤ 4 (√x² + y²)² + y² ≤ 4 i teraz powinno wyjść mi równanie okręgu... x² + y² + y² ≤ 4 x² + 2y² ≤ 4 tylko nie wiem co zrobić z tą dwójką przy y². ? Pozdrawiam Dominika

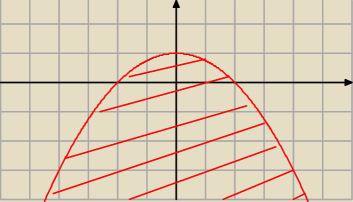
g: Nie wyszło Ci podnoszenie do kwadratu: (√x²+y²+y)² ≠ (√x²+y²)²+y². √x²+y² ≤ 2−y (y ≤ 2) x²+y² ≤ 4−4y+y² y ≤ 1−x²/4

Dominika: Faktycznie, głupi błąd. dziękuję Ci bardzo!

Dominika: Mam jeszcze niepewności w tym przykładzie: |z−2|≤2 zrobiłam tak: |x+yi−2|≤2 |x−2+yi|≤2 √(x−2²)+y² ≤2 / (...)² (x−2)²+y² ≤4 x²−4x+y² ≤0 /√ x−2√x+y ≤0 czy wzór funkcji to y≤ 2√x−x ? Jaka to jest funkcja?

g: Błąd: √x²−4x+y² ≠ x−2√x+y

Jerzy: To koło o środku S(2;0) i promieniu r = √2

Jerzy: |z − z₀I ≤ a − to ziór punktów, których odległość od punktu z₀ jest nie wieksza niż a.

Dominika: g, dzięki rzeczywiście nie zniesie się ten kwadrat przez pierwiastkowanie Jerzy, po czym rozpoznam, że jest to koło? mi wyszło równanie x² − 4x + y² ≤ 0. Czy tutaj jest to ukryte? Czy od razu w |z−2| ≤ 2 widać, że to koło ? Pozdrawiam

Pytający: Widać od razu, patrz post Jerzego z 14:59. |z−(5+2i)|≤4 // koło o środku S(5;2) i promieniu r=4 |z+i|<3 // koło (minus okrąg, bo nierówność ostra) o środku S(0,−1) i promieniu r=3 |z−2| ≤ 2 // koło o środku S(2;0) i promieniu r=2

Jerzy: x² − 4x + y² ≤ 0 ⇔ ( x − 2)² + (y − 0)² ≤ 2² I masz koło S(2,0) i r = 2 ( wyżej się pomyliłem )

Dominika: Czyli mam rozumieć, że |z−z₀| ≤ a to po prostu jest taki wzór i nie muszę podstawiać nic za "z" i liczyć modułu, podnosić do kwadratu itd.. ? Niestety nie mieliśmy na zajęciach wprowadzonej tej "właściwości" czy jak to nazwać ; −) Dziękuję Wam bardzo i pozdrawiam

AiO: Ale Dominiko taka sama wlasnosc na modul . A o tym to uczylas sie w liceum

AiO: Chodzilo mi o wartosc bezwzgledna