wykaz ze mateo: wykaz ze dla kazdej liczby rzeczywistej x prawdziwa jest nierownosc x(x−1)(x−2)(x−3)+1≥0 Moje pytanie jest takie iz wiem ze jak to wszystko wymnoze to bede mogl wyliczyc pochodna i jej msc zerowe i do tego ekstrema lokalne ale moje pytanie brzmi czy nie wystarczyłoby po wymnozeniu obliczyc sama granice w −nies i w +niesk ?

Adam: samo to nie wystarczy x(x−3)(x−1)(x−2)+1=(x²−3x)(x²−3x+2)+1= =(x²−3x+1−1)(x²−3x+1+1)+1=(x²−3x+1)²−1²+1=(x²−3x+1)²≥0

mateo: a w takim razie sama pochodna wystarczy bez liczenia granicy ?

mateo: bo wlasnie nie rozumiem sensu licznia granicy jak juz zanm minimalne ekstremum

Adam: sama pochodna wystarczy, ale zależy jak z niej skorzystasz

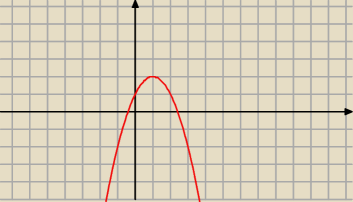
po prostu Michał: ekstremum mamy np. w punkcie P(1,2) , natomiast granice pokazuja, ze funkcja "leci" w − ∞

mateo: juz rozumiem bo moze byc taka sytuacja ze mam sobie funkcje gdzie zaczyna sie w + nsk ma gdzies tam sobie min lokalne ponad osia ale nagle opada na −nsk

Adam: po prostu Michał jakbyś policzył pochodną to byś zobaczył że f'(x)>0 dla x<1 więc w tym przypadku trzeba byłoby liczyć granice w ±∞ tutaj jednak jest inaczej

mateo: dziekuje bardzo za pomoc

po prostu Michał: no tak, ale w tego typu zadaniach to wiadomo ze latwiej przeksztalcic do zapisu (...)²