wektory PrzyszlyMakler: Wektor u ma dodatnie współrzedne i długość 10. Jest on prostopadły do prostej 3x + 4y − 8 = 0 Wyznacz u. u = [A,B] prosta 3x + 4y −8=0 ! Nie wiem czy tak można, ale warunek prostopadłości A₁A₂ + B₁B₂= 0 3A + 4B = 0 3A = −4B A=−4/3B i pitagoras

	4
√(−		B)2 + B2 = 10
	3

niestety wychodzi źle. Jak to zrobić, dlaczego źle? Proszę o pomoc i o wskazówki i jakieś rady naukowe dotyczące wektorów, słabo z nimi u mnie

PrzyszlyMakler: oczywiscie mial być długi pierwiastek

Leo: A,B >0 i A=−4/3B się wyklucza

PrzyszlyMakler: to jak to zrobić?

Adam: wektor <3; 4> jest normalny do prostej prostopadły do niej u=<3k; 4k>

PrzyszlyMakler: Adam, wytłumaczyłbyś mi jak to działa? Bo w końcu ten warunek..

Leo: narysuj sobie tę funckje liniową zauważ, że działa jak wektor [−3,4] albo [3,−4]

Adam: wektor wodzący prostej to by był taki x=k to y=(−3/4)k+2 czyli wektor wodzący (równoległy) to byłby <4k; −3k> wektor normalny (zawsze to jest ten przy współczynnikach x, y) to za to <3; 4> masz jakiś wektor <3k; 4k> i wyliczasz k, k=2

Leo: adam. to chyba warunek równoległości, czy się myle ?

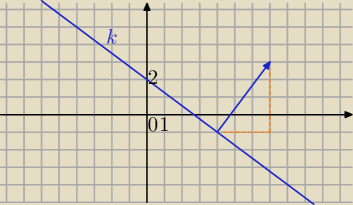
Mila: k: 3x + 4y − 8 = 0 to jest równanie prostej w postaci ogólnej. wektor prostopadły do prostej k to : v^→=[3,4] |v|=√3²+4²=5 u^→=[6,8] lub [−6,−8]

Adam: później, już na studiach, zobaczysz że równanie płaszczyzny to ax+by+cz+d=0 i wektor normalny czyli prostopadły to niej to zawsze <a; b; c> tutaj jest analogicznie

Leo: a to zwracam honor

PrzyszlyMakler: Milo, a dlaczego napisałaś, = 5, a nie 10?

PrzyszlyMakler: A OK, nie ważne... Ty obliczyłaś pierwiastek z 25, ok..

Adam: √3²+4²=10 ?

Mila: v=[3,4] |v|=√3²+4²=√9+16=√25=5 długość wektora v u=[6,8] |u|=√6²+8²=√36+64=√100=10

PrzyszlyMakler: Czyli reasumując: do prostej Ax By + C=0 Wektor prostopadły do tej prostej ma współrzędne [Ak, Bk] Wektor równoległy do tej prostej ma współrzedne [Bk,Ak] I jak mam wektor z= [A,B] to wektor prostopadły do tego wektora ma współrzedne [−Bk,Ak] a równoległy [Ak, Bk] wszystko poprawnie?

Mila: Zaraz.

Metis: matematyka.pisz.pl/strona/1214.html Nie mąć już sobie w głowie. Odpocznij od cyferek, to pomoże bardziej od rozwiązywania jeszcze zadanek.

Mila: Ax+By+C=0 równanie ogólne prostej [A,B] − wektor prostopadły do prostej [kA,kB] || [A,B] , k≠0 [−B,A] ⊥| [A,B] [B,−A] ⊥| [A,B] =============== k: 3x+5y+8=0 i m: 5x−3y+D =0 proste prostopadłe k: 3x+5y+8=0 i 3x+5y+10=0 proste równoległe

PrzyszlyMakler: Dziękuję za wszystko Milu bardzo mi się coś takiego przyda. A zechcesz mi jeszcze wyjaśnić, jak Ty rozwiązywałaś to zadanie 22:42? Bo obliczyłaś najpierw długość wektora o jednostce (?) 1 Chodzi o to, że w ogółle nie posługiwałas się parametrem "k"

Mila: Może jutro to wyjaśnimy z przykładami, dzisiaj Dobranoc Też idź spać, abyś jutro miał jasny umysł.

PrzyszlyMakler: Ok, dzięki za wszystko!

PrzyszlyMakler: Wektor równoległy do prostej o rownaniu y=7/24x +4 o dodatnich współrzędnych długości 10. Wychodzi mi dobrze [−9,6 , 2,8 ] Ale wynik na minusie. To mogę tak bez uzasadnienia przemienić na plus bo tego chcieli w zadaniu ?

PrzyszlyMakler: refresh

Mila:

	7
k:		x−y+4=0 /*24
	24

7x−24y+96=0 [7,−24] ⊥k a^→=[24,7] ||k szukamy wektora równoległego do a^→ o długości 10. b=[24k,7k] i k>0 √(24k)²+(7k)²=√576k²+49k²=10² 625k²=100

	100
k2=		i k>0
	625

	10		2
k=		=		=0,4
	25		5

b=[24*0,4;7*0,4] b=[9,6; 2,8]

PrzyszlyMakler: Wektor równoległy do prostej jest więc postaci [−B, A]?

PrzyszlyMakler: Proszę o odpowiedź

Mila: Tak, lub [B,−A] zależy od sytuacji znakowej w równaniu ogólnym.

PrzyszlyMakler: Kiedy będzie tak A Kiedy tak ?

Adamm: PrzyszłyMakler, oba są równoległe różnią się jedynie zwrotem

Mila: W zależności od potrzeb. Możesz mieć takie polecenie jak w poprzednim zadaniu. Np. taki problem: dana prosta k: k: 2x+5y−6=0 [2,5] −wektor prostopadły do prostej k Prosta prostopadła do k : m: 5x−2y+D=0 , D wyznaczysz, gdy będziesz miał wsp. punktu przez który przechodzi nowa prosta. m⊥k Ale możesz zapisać tak: −5x+2y+D=0 ja wolę, gdy przy x jest dodatni wsp. Jednak to jest ta sama prosta .

Metis: Robisz sobie krzywdę Przyszły Pamiętam gdy uczyłem się w ciągu kilku dni bez przerwy do kolokwium z AM, na kolokwium miałem dość cyferek i praktycznie nie myślałem.

PrzyszlyMakler: Ogarniam. Dziękuję Mila. Spoko Metis, już się nie uczę wracam tylko do zadań które kiedyś mnie pokonały I ogarniam wektory bo je słabo umiem A nigdy czegoś takiego na maturze nie było.

Metis: Powodzenia