dowody PrzyszlyMakler: Witam, trochę nie rozumiem idei prowadzenia dowodów z liczbami a,b gdzie któraś z liczb jest parametrem, przejdźmy do przykładu. Udowodnij, że dla liczb dodanich a i b, niewiększych od 1, prawdziwa jest nierówność

	1
ab2 −a2b ≤
	4

f(b) = b²a − ba² b ∊ (0;1>

	1
f(0) = 0 ≤
	4

f(1) = a−a² a ∊ (0;1> dla a = 0

	1
f(1) = 0 ≤
	4

dla a = 1

	1
f(1) = 0 ≤
	4

f(b) = b²a − ba²

	a2		a
bw =		=
	2a		2

	a
f(		)= .. i trochę nawet nie wiem jak to dalej zrobić, o co chodzi w takim sposobie? jak
	2

się za to zabrać? zawsze można w ten sposób przeprowadizć dowód?=> kiedy nie można?

Omikron: Jeżeli wiadomo że D=(0,1> udowodnij że dla każdej wartości parametru m z przedziału (0,1> funkcja f(x)=mx²−m²x przyjmuje wartości niewiększe niż 1/4. A przy takim poleceniu potrafisz to sobie lepiej wyobrazić?

PrzyszlyMakler: Może i umiem, ale ja nie rozumiem jak to możliwe, że to działa z liczbami a,b XD. No może niby nie mam rozumieć, tylko wiedzieć, ale chciałbym rozumieć. ponieważ m>0 ramiona paraboli skierowane ku górze, więc wartość najmniejsza jest w wierzchołku

	1
Xw =
	2

	1		1		1		1
f(1/2) =		m −		m2 = −		m2 +		m <−−− I to trzeba potratkować jako
	4		2		2		4

kolejną funkcję i sprawdzić ja na przedziale (0;1>? f(0) = 0 f(1) = 0

Omikron: Ale Ty szukasz największej wartości. Największa będzie najdalej od wierzchołka

PrzyszlyMakler:

	1
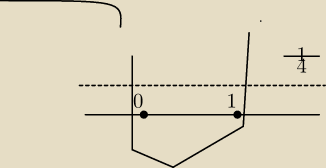
należy udowodnić, że funkcja przyjmuje wartości ≤
	4

załóżmy, że ta funkcja wygląda tak jak narysowałem, to wydaje mi się, że należy obliczyć wartości dla argumentów 0,1 i wierzchołka, jeżeli wierzhcołek się zawiera w przedziale (0;1>

PrzyszlyMakler: Aha, w sumie to wartosc w wierzcholku mi nie potrzebna, bo na pewno jest ona mniejsza niż dla argumentów 0 i 1

PrzyszlyMakler: Pomoze ktos dokonczyc? Czy to skonczone bez rozpatrywania wierzchołka?

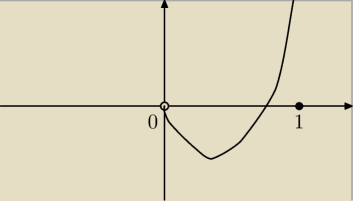
Omikron: Można podpierając się rysunkiem zauważyć, że największa wartość będzie w 1. f(1)=m−m²=m(1−m) Czyli rzeczywiście mamy drugą funkcję, którą musimy rozpatrywać: g(m)=m(1−m) Bo teraz musimy sprawdzić, kiedy ta funkcja będzie przyjmować największą wartość. a<0, największa wartość w wierzchołku, czyli w 1/2 g(1/2)=1/4, więc największą wartością przyjmowaną przez funkcję f(x) w danym przedziale jest 1/4. To jest takie trochę nietypowe zadanie na rozwiązywanie w ten sposób, zwykle można łatwo przez pochodną i ekstrema, a tutaj jest problem z ograniczeniem dziedziny w 1, ale da się mimo wszystko.

Omikron: Największa wartość w 1, bo z założeń m<1 (a m jest miejscem zerowym), czyli funkcja przekroczy oś odciętych na lewo od 1.

PrzyszlyMakler: Ok, dzięki, chyba rozumiem, jeszcze poanalizuje. Da się jeszcze poprzez nierownosci miedzy srednimi i komentarze odnosnie iloczynu i roznicy, ale chcialem sprobowac tym sposobem, bo on jest bardzo uniwersalny

Omikron: Często da się go zastosować, ale nie zawsze np. jeżeli będą cztery niewiadome lub wysokie potęgi.