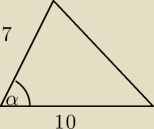
trojkąty wojtek: pole trojkata o bokach 7 i 10 jest rowne 10√6 wowczas pozostaly bok tego trojkata moze miec rownosc

	17
A)		√6
	4

B).9 C)3√6 D)7 probowałem to zrobić wzorem na pole P=1/2 a*b*sin alfa i wyszlo mi 10√6=35sinalfa sinalfa= 10√6/35 ≈0,699 czyli cos alfa=45 i dalej tw. cosinusow, ale wynik to 5√2 dlaczego tą metodą nie wyszedł mi dobry wynik?

po prostu Michał: bo cos alfa na pewno nie wynosi 45.

po prostu Michał:

	1
P =		* 7 * 10 * sin α = 10√6
	2

35 sin α = 10√6

	10√6		2√6
sin α =		=
	35		7

teraz z jedynki tryg. sin²α + cos²α = 1

	24		25
cos2 α = 1 − sin2α = 1 −		=
	49		49

	5
cos α =		(jesli zalozymy ze trojkat jest ostrokatny)
	7

z tw. cos. c² = 7² + 10² − 2*7*10*cos α

	5
c2 = 149−140*
	7

c² = 149−100 = 49 c = 7

wojtek: a ja poszedłem na skróty i 2√6/7 wyszlo mi 0.6998 i z tablic wartosci geometrycnzych wziąłem, sin 45 bo na oko zobaczylem, ze 0,7071 ma bliżej do 0,6998 niż 0,6947, a tak to wszystko by się zgadzało

po prostu Michał: z przyblizeniami tez by wyszlo, gdybys wzial cos α = 0,7071 , a nie 45^o, bo przeciez α ≈ 45^o, a nie cosinus tego kata.

wojtek: nie wyszło by

po prostu Michał: wyszlo by ≈ 7,0714920632070287292180716052427 a to juz bys sie domyslil, ze chodzi o liczbe "7"

wojtek: Dzięki, jak tak patrzę na twoje obliczenia to sobie myślę że jesteś prze chuj