Zespolone Warczek: Przedstawić na płaszczyźnie zespolonej: |z+1|+ |z−j|=4 Podstawiam z = x+iy po wyliczeniu modułów wychodzi mi: (x+1)² +y² + x² +(y−1)² =16 i na tym etapie nie wiem jak to zwinąć to równania okręgu

astro: Najpierw sie zastanów czym by było |z+1|=4 na płaszczyźnie?

Warczek: Okrąg o punktach −1;0 i promień 16

astro: i promień 4, tak

astro: no to co to może być |z+1|+|z−i|=4

Warczek: a przepraszam promień 4. dwa okręgi ?

astro: eeee no nie ma tak łatwo

astro: Zacznijmy tak po twojemu (x+1)²+y²+x²+(y−1)²=16 x²+2x+1+y²+x²+y²−2y+1=16 2x²+2x+2y²−2y=14 x²+x+y²−y=14 (x+0.5)²+(y−0.5)² =14 −2*0.5²

astro: (x+0.5)²+(y−0.5)²=√13.5²

Warczek: Trzecie równanie − gdzie uciekły te dwójki?

astro: podzielilem obie strony przez 2, tak − powinno byc potem 7 po prawej stronie

astro: (x+0.5)²+(y−0.5)²=√6.5²

Warczek: I znowu łatwe zadanie, a człowiek się męczy Dzięki wielkie za uświadomienie chyba czas zacząć weekend. Miłego wieczoru życzę!

astro: Również!

Biedny Student:

|z+1
	<1
|z−1

to wyjdzie x < 0 ?

astro: to już jes troche cos innego |z+1|<|z−1|

Mila: Błędne rachunki kolego. To będzie elipsa. x,y∊R √(x+1)²+y²+√(x²+(y−1)²=4⇔ √(x+1)²+y²=4−√(x²+(y−1)² /² x²+2x+1+y²=16−8√x²+y²−2y+1+x²+y²−2y+1 2x+1=17−8√x²+y²−2y+1−2y⇔ 2x+2y=16−8√x²+y²−2y+1 /:2 x+y−8=−4√x²+y²−2y+1 8−x−y=4√x²+y²−2y+1 /² 8>x+y 64+x²+y²−16x−16y+2xy=16(x²+y²−2y+1) 15x²−2xy+16x+15y²−16y=48 Tu jest problem z wyrazem 2xy, trzeba pokombinować , aby przekształcić do postaci kanonicznej. Jest jeszcze inny sposób. .

astro: tak, masz racje, tak by blo gdyby te moduły byly do kwadratu, przepisalem za tobą

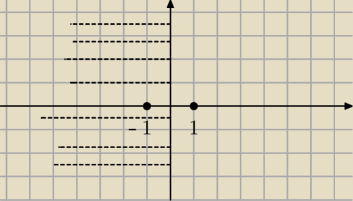
Jerzy: Bez osi OY.

Jerzy: To rysunek do 19:08.

Mila:

|z+1|
	<1
|z−1|

z≠1 |z+1|<|z−1| [ równanie |z+1|=|z−1| − równanie symetralnej odcinka o końcach (−1,0) i (1,0), czyli Oś OY, x=0, Interesujące nas punkty leżą po jednej stronie symetralnej− z lewej ] Albo rachunki: √(x+1)²+y²<√(x−1)²+y² /² x²+2x+1+y²<x²−2x+1+y² 2x+1<−2x+1 4x<0 x<0 wszystko po lewej stronie OY

Jerzy: Witaj Milu Czyżby rysunek tego nie pokazywał ?

Mila: Cześć Jerzy, nie pamiętasz jak napisać równanie elipsy mając pewne dane, albo podaj linka.

Mila: Twój rysunek Jerzy to pokazuje, ale pisałam, gdy go nie było i trochę się rozpisałam, jak to "baba" gadatliwa.

Jerzy: Dawno nie bawiłem się w te klocki ( elipsa )

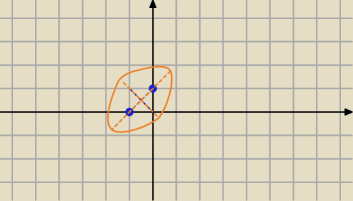
Mila: Może tak : |z+1|+ |z−j|=4 korzystając z tego równania narysować elipsę: ogniska: (−1,0) (0,1) 2a=4 , a=2

	√2
2c=√2 , c=
	2

c=√a²−b²

√2		1
	=√22−b2⇔		=4−b2
2		2

	7		√14
b2=		, b=
	2		2