ddd
Xxxx: Witam !
| | x | |
Mam zbadać monotoniczność funkcji |
| . |
| | x2−9 | |
| | x2+9 | |
Obliczyłem pochodną y' = − |
| |
| | (x2−9)2 | |
f'(x) = 0
i wychodzi mi −x
2=9 , nwm co robić dalej.
5 maj 18:22
Jerzy:
A do czego ci potrzebne miejsce zerowe pochodnej?
5 maj 18:52
Xxxx: Właściwie to jest niepotrzebne

Ale jak liczę nierówności np. dla f'(x) >0
to i tak wychodzi −x
2 > 9 i jak z tego mam wyznaczyć kiedy funkcja rośnie

5 maj 19:39
Jerzy:
Zauważ,że ułamek jest stale dodatni, a zatem pochodna stale .... ?
5 maj 19:40
Xxxx: −x
2−9<0
−[(x−3)(x+3)]<0
Więc będzie malejąca ? Nie za bardzo pamiętam jak się robiło tą monotoniczność

5 maj 19:50
Jerzy:
Ponieważ przed ułamkiem jest minus, więc pochodna jest stale ujemna,
a zatem funkcja jest stale malejąca. Koniec zadania.
5 maj 19:51
Xxxx: Dzięki wielkie Jerzy

Widzę, że jeszcze bd musiał przerobić parę przykładów.
5 maj 19:52
Janek191:
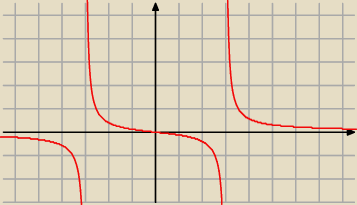

?
5 maj 19:53
Xxxx: Tak jak u Janka miał wyglądać wykres

Jeszcze raz dziękuje wszystkim za pomoc.
7 maj 11:36
 Ale jak liczę nierówności np. dla f'(x) >0
to i tak wychodzi −x2 > 9 i jak z tego mam wyznaczyć kiedy funkcja rośnie
Ale jak liczę nierówności np. dla f'(x) >0
to i tak wychodzi −x2 > 9 i jak z tego mam wyznaczyć kiedy funkcja rośnie

 Widzę, że jeszcze bd musiał przerobić parę przykładów.
Widzę, że jeszcze bd musiał przerobić parę przykładów.

 ?
?
 Jeszcze raz dziękuje wszystkim za pomoc.
Jeszcze raz dziękuje wszystkim za pomoc.