W rombie o boku długości a W4RI0T: W rombie o boku długości a i kącie ostrym α poprowadzono z wierzchołka kąta ostrego odcinki do przeciwległych boków tak, że podzieliły one rąb na 5 części o równych polach. Oblicz długości tych odcinków.

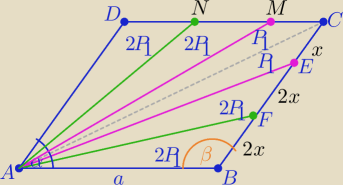
Eta: Z treści zadania: ( równości pól i z symetrii względem przekątnej AC

	2		1
|BF|=|FE|=		a i |CE|=		a
	5		5

z twierdzenia kosinusów ( oraz cosβ= −cosα) w ΔAEB :

	16		4
|AE|2=a2+		a2+2*a*		a*cosα ⇒ .... |AE|=|AM|= ...
	25		5

i analogicznie w ΔAFB

	4		2
|AF|2= a2+		a2+2*a*		a*cosα ⇒ ........
	25		5

W4RI0T: Wow, dzięki