matura a: Odp. matura 2017 matematyka

	1		1		5
1. 58 * 16−2 = 58 *		= 58 *		= (		)8
	162		28		2

a: 2. ³√54 − ³√2 = ³√27*2 − ³√2 = 3³√2 − ³√2 = 2³√2

a: 3.

	9
2log23 − 2log25 = log29 − log2 25 = log2(		)
	25

a: 4. liczba wzrosla o 120% czyli jak bylo x, to teraz jest x + 1,2x = 2,2x. 2,2x = 8910

	8910
x =		= 4050
	2,2

a: 5. Najszybciej podstawiajac. sprawdzmy wpierw dla x=−1 (bo jedynka najprostsza liczba) (−√2−2)² = (2+√2)² (√2+2)² = (2+√2)² nierownosc prawdizwa dla x=−1 nie ma co dalej sprawdzac.

a: 6. (x⁴+1)(2−x) > 0 (x⁴+1) jest zawsze >0 zatem 2−x>0 −−> x < 2 nie pasuje liczba " 3 "

a: 7. 2−3x ≥ 4 3x ≤ −2

	2
x ≤ −
	3

odp. A

a: 8. x(x²−4)(x²+4) = 0 x = 0 lub x² − 4 = 0 lub x² + 4 = 0 x = 0 lub (x−2)(x+2) = 0 x = 0 lub x = − 2 lub x = 2 mamy 3 rozwiazania. odp. A

a: 9. f(x) = √3(x+1)−12 f(x) = 0 ⇔ √3(x+1)−12 = 0 √3x + √3 = 12 √3x = 12 − √3

	12−√3		12		12√3
x =		=		− 1 =		− 1 = 4√3 − 1
	√3		√3		3

odp. D

a: 10. f(x) = ax²+bx+c miejsca zerowe to −3 i 1 f(x) = a(x+3)(x−1) podstawiajac wspolrzedne wierzcholka : 4 = a(−1+3)(−1−1) 4 = a(2)(−2) a = − 1 f(x) = −1(x+3)(x−1) = −1(x²+2x−3) = −x² −2x + 3 wspolczynnik c = 3 odp. A

StrasznyNieogar: 4 zle

a: 11. f(x) = a^x, wiemy, ze nalezy punkt A=(1,2) , zatem 2 = a¹ a = 2 odp. B

a: 12. ciag arytmetyczny, zatem a₁ = 5 a₂ = 11 = a₁ +r 11 = 5 + r −−−> r = 11−5=6 obliczamy podstawiajac do odp. a₁₀ = a₁ + 9r = 5 + 9*6 = 5+ 54 = 59 −> nie zgadza sie wszystkie odp. to 71 zatem najszybciej sprawdzic ile szostek trzeba dodac do 59 aby miec 71 71 − 59 = 12 czyli dwie szostki odp. to a₁₂ zatem C)

a: 13. 24,6,a−1 −−> geometr. 6² = 24(a−1) 36 = 24a − 24

	36+24		60		10		5
a =		=		=		=
	24		24		4		2

odp. B

a: 14. m = sin(50^o) ze wzorow redukcyjnych wiadomo, ze sin α = cos(90−α) zatem sin(50) = cos(90−50) = cos 40 odp. C

a: 15. trojkat oparty na srednicy a wiec, miara przy wierzcholku C wynosi 90 stopni (lacznie) zatem kat OCB ma miare 90−56 = 34 jako ze OBC to trojkat rownoramienny, to α = 180 − 2*34 = 112 odp. D

a: 16. z podobienstwa trojkatow

|BD|		|BC|
	=
|DE|		|AC|

10		12
	=
|DE|		24

12|DE| = 240 |DE| = 20 odp. A

a: 17. jest to trojkat ekierka, zatem obwod to a+2a+a√3 = 3a+a√3 = a(3+√3) odp. D

a: 18.

	3
tg α =
	2

odp. A

Test: Jak tangens może dodatni wyjść w 2 cwiartce

a: 18. (poprawka) oczywiscie −3 tam jest, zatem

	−3
tg α =
	2

odp. C

a: 19. proste przecinaja sie pod katem prostym, zatem sa prostopadle. prosta l: y = ax + b 4 = a(−2) +b −−> b = 4 + 2a zatem rownanie prostej l: y = ax + 2a + 4 proste prostopadle, gdy a₁ * a₂ = − 1

	1
(−		) * a = − 1
	4

a = 4 zatem prosta l: y = 4x + 8 + 4 = 4x + 12 odp. A

a: 20. rownanie okregu to (x−2)² + (y−3)² = 25 podstawiamy odp. (rozmyslnie, tzn. suma kwadratow jakich liczb da 25 ?) 16+9 to pierwsza mysl, zatem podstawiamy najpierw odp. C (−1−2)² + (7−3)² = 25 9 + 16 = 25 zgadza sie poprawna odp. C

a: 21. niech krawedz podstawy bedzie "a" wtedy wysokosc = 3a P_c = 140 = 2*a² + 4*a*3a = 2a² + 12a² = 14a²

	140
a2 =		= 10
	14

a = √10 odp. B

a: 22. skoro wysokosc walca jest rowna promieniowi, to trojkat OSA jest rownoramienny

	90
oraz prostokatny, zatem kat OAS ma miare		= 45
	2

	√2
sinus 45 =
	2

odp. C

a: 23. h = 4 promien podstawy r = 6

	1		1
V =		* π * r2 * h =		* π * 36 * 4 = 48π
	3		3

odp. A

a: 24.

3+5+7+9+x+15+17+19
	= 11
8

75 + x = 88 x = 13 odp. B

a: 25. dzielniki liczby 24: 1,2,3,4,6,8,12,24 jest ich lacznie 8

	8		1
prawdopodobienstwo zdarzenia A wynosi		=
	24		3

odp. C

Dawid: Przeanalizuj jeszcze raz czwarte i napisz odpowiedź, no bo wzrosła o 120% w stosunku do wszystkich zwierząt, a nie tylko tych zagrożonych, mhm

a: 26. 8x² − 72x ≤ 0 /:8 x² − 9x ≤ 0 x(x−9) ≤ 0 x ∊ <0;9>

a: jeszcze raz czwarte to za chwile, wpierw skoncze te. 27. wykazac ze tamta liczba podzielna przez 17. 4²⁰¹⁷ + 4²⁰¹⁸ + 4²⁰¹⁹ + 4²⁰²⁰ = = 4²⁰¹⁷(1+4) + 4²⁰¹⁹(1+4) = = 5(4²⁰¹⁷+4²⁰¹⁹) = 5(4²⁰¹⁷(1+16)) = 5*4²⁰¹⁷*17 = 17k, k ∊ C koniec dowodu [=]

Jerzy: @Dawid ... a gdzie jest napisane do wszystkich zwierząt ? ( czytaj uważnie treść zadań)

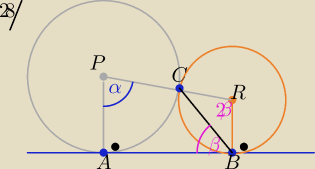
a: 28. skoro ta prosta jest styczna to katy PAB oraz RBA sa proste. trojkat PCA oraz trojkat RCB sa rownoramienny, (boki to promienie okregow) figura ABRP jest trapezem, bo okregi sa styczne zewnetrznie, a prosta jest styczna do okregow w punktach A i B. kat CBR ma miare 90 − β tak samo kat BCR. −> 90 − β w zwiazku z tym kat przy wierzcholku R (kat CRB) ma miare 180 − (90−β) − (90 − β) = 2 β zatem kąt α ma miare 360 − 2*90 (katy przy A i B) − 2β (kat przy R) = = 360 − 180 − 2β = 180−2β c.n.w. [=]

a: 29. f(x) = ax²+bx+c

	3
najwieksza warosc jest rowna 6, oraz f(−6)=f(0) =
	2

zatem, wiemy, ze

	3
f(−6) =		= 36a − 6b + c
	2

	3
f(0) =		= c
	2

podstawiajac z powrotem te "c" do f(−6)

3		3
	= 36a − 6b +
2		2

zatem 36a−6b = 0 −−−> b = 6a stad mamy rownanie naszej funkcji

	3
f(x) = ax2 + 6ax +
	2

skoro ma najwieksza wartosc , a jest to parabola, to ramiona sa skierowane w dol. wiec ta najwieksza wartosc jest w wierzcholku.

	−6a
p =		= 3
	2a

wiemy, ze f(3) = 6 (bo najwieksza wartosc jest rowna 6)

	3
f(3) = 9a + 18a +		= 6
	2

	3
27a = 6 −
	2

	9
27a =
	2

	9		1		1
a =		=		=
	2*27		2*3		6

Jerzy: 33) |Ω| = 90 |A| = 10

	10		1
P(A) =		=
	90		9

Test: Jak Ci wychodzi dodatnie a jak parabola ma ramiona do dołu?

Ewa1: W 29 będzie −1/2

a: 30. niech przeciwprostokatna bedzie "c" , krotsza przyprostokatna "a", dluzsza przyprostokatna "b" wtedy c = 26 a = x (jakas niewiadoma, nie trzeba wprowadzac, ale ja wprowadze) b = 14+x z pitagorasa obliczamy "x" 26² = x² + (14+x)² 676 = x² + (196 + 28x + x²) 676 = 2x² + 28x + 196 2x² + 28x − 480 = 0 x² + 24x − 240 = 0 Δ = 24² + 4*240 = 576 + 960 = 1536 √Δ = √1536 = √256*6 = 16√6

	−24 − 16√6
x1 =		< 0 −−−> przypadek odpada, bo bok nie moze byc < 0
	2

	−24+16√6
x2 =		= −12 + 8√6 > 0
	2

zatem boki : c = 26 a = 8√6−12 b = 14 + 8√6−12 = 2+8√6 Obwod = 2+8√6 + 8√6−12 + 26 = 16√6 + 16

a: AD 29. p = −3 oczywiscie.

	3		3
f(−3) = 9a − 18a+		= −9a +
	2		2

f(−3) = 6, zatem

	3
−9a +		= 6
	2

	3
−9a = 6 −
	2

	9
−9a =
	2

	9		1
a = −		= −
	2*9		2

============= przepraszam za blad.

StrasznyNieogar: x² + 14x − 240 14 a nie 24

Aaa: 30 błąd

StrasznyNieogar: Ob = 60

a: 31. [Ciag arytmetyczny] a₁ = 8 S₃ = 33 musimy obliczyc a₁₆−a₁₃ zatem, wiemy, ze

	a1+a3
33 =		* 3
	2

	8+a3
33 =		*3
	2

22 = 8+a₃ −−−> a₃ = 14 wiemy natomiast, ze a₃ = a₁ + 2r zatem

	14−8
14 = 8 + 2r −−−> r =		= 3
	2

a₁₆ = a₁ + 15r a₁₃ = a₁ + 12r a₁₆−a₁₃ = a₁ + 15r − (a₁+12r) = 15r − 12r = 3r = 3*3 = 9

Jerzy: 31)

	2*8 + 2r
33 =		*3 ⇔ 22 = 16 + 2r ⇔ r = 3
	2

a₁₆ = 8 + 15*3 = 53 a₁₃ = 8 + 12*3 = 44 a₁₆ − a₁₃ = 53 − 44 = 9

relaa: 29.

	−6 + 0
Wiedząc, że f(−6) = f(0) to xw =		= −3 oraz yw = 6, więc
	2

f(x) = a(x + 3)² + 6

	3
a(0 + 3)2 + 6 =
	2

	9		1
9a = −		⇒ a = −
	2		2

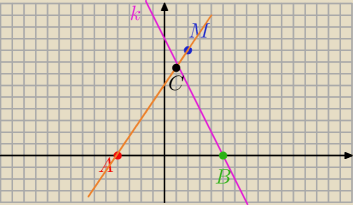
a: 32. prosta k przecna os Ox w punkcie : −2x+10 = 0 x = 5 prosta AM :

	9−0		9		3
aAM =		=		=
	2+4		6		2

	3		3
y =		(x+4) + 0 =		x + 6
	2		2

miejsce przeciecia sie AM z prosta k :

3
	x + 6 = −2x+10 /*2
2

3x + 12 = −4x + 20 7x = 8

	8
x =
	7

	8		16		54
y = −2*		+10 = −		+ 10 =
	7		7		7

	8		54
zatem punkt C(		,		)
	7		7

pole trojkata mozna obliczyc np. ze wzoru w kartach znajac wspolrzedne wierzcholkow jednakze mozna prosciej, gdyz odleglosc od C do odcinka AB (pod katem prostym) to nic innego jak jego

	54
wspolrzedna igrekowa, czyli
	7

zatem

	1
do wzoru P=		a*h
	2

	54
h =
	7

a = |AB| = |−4| + |5| = 4+5 = 9

	1		54		243
czyli P =		*		* 9 =
	2		7		7

a:

	5√3
h =
	4

	a*h		15√3
Pb = 3 *		=
	2		4

3		5√3		15√3
	* a *		=
2		4		4

3
	a * 5 = 15
2

	2
a = 3 *		= 2
	3

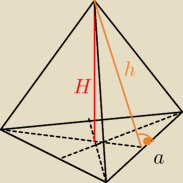
1		1		a√3		1		2√3		√3
	* hpodstawy =		*		=		*		=
3		3		2		3		2		3

z pitagorasa :

	1
H2 + (		hpodstawy)2 = h2
	3

	25*3		3		75		1
H2 =		−		=		−
	16		9		16		3

	225−16
H2 =
	48

	209
H = √
	48

	1		a2√3		1		4√3		209
V =		*		* H =		*		* √		=
	3		4		3		4		48

	√3		209		1		209		√209
=		* √		=		* √		=
	3		48		√3		48		12

.:

a: wiec tak, 30 blad w rownaniu kwadratowym, ale to kazdy da rade natomiast co do zadania 4...

Mix: czwarte masz dobrze

a: a no to fajnie.

tomek: zad 34. skoro wysokość ściany bocznej jest prostopadła do krawędzi podstawy to nie powinna ona też być wysokościa całego ostrosłupa...

tade: prostopadła do krawedzi a nie do płaszczyzny podstawy

tomek: jeżeli jest prostopadła do krawędzi to musi być jednocześnie do płaszczyzny podstawy..

tomek: wysokość zawsze musi padać pod kątem prostym

Mix: tu chodzi o sciane boczną nie o ostrosłup

Mix: zgadza sie pada pod kątem prostym do krawedzi podstawy ale jest nachylona do PŁASZCZYZNY podstawy

prsa: A co w przypadku gdy w zadaniu 32 wzor prostej y=−2x+10, ktos zle przepisal i liczyl dla y=2x+10

.: specjalnie dla ciebie zrobią wyjątek oczywiste, odejmą ci punkty, albo unieważnią

StrasznyNieogar: Sierpień

prsa: O czym wy wg piszecie? Tu przyklad − Kryteria oceniania 2016 Przyklad 3)Kryteria oceniania − matematyka 2015 "Jesli zdajacy otrzyma inne rownanie kwadratowe np v²+9v−4536=0 zamiast równania v²−9v−4536=0 ( NP. W Wyniku ZLEGO PRZEPISANIA ZNAKU LUB LICZBY), konsekwentnie jednak rozwiaze otrzymane rowannie kwadratowe, odrzuci ujemne rozwiania i pozostaw wynik, ktory moze byc realna predkoscia jednego z pociagow, to takie rozwiązanie kwalifikujemy do kategorii Rozwiazanie pelne i przyznajmy 5pkt."

Zażyty: a jak ktoś zrobił błąd w ostatnim zamiast a=2, napisał a=1 (bład na początku) to ile może się spodziewać punktów 0?

Zażyty: tzn. źle napisałem wzór na pole trójkąta zamiast 1/2ah napisałem ah i wyszło mi połowę mniej

prsa: Patrzac po kryteriach oceniania z ubiegłych lat za kazdy etap zadania jest przyznawany punkt. Mysle ze jestli za to otrzymasz 0 (za blad w obliczeniu a), a dalsze obliczenia zalezaly od a to spodziewalbym sie raczej 0 badz 1 punktu. Ale komentarze typu "Sierpien" nie sa zdecydowanie na miejscu. Pozdrawiam

Eta: 29/ y=ax²+bx+c

	3		0−6		3
q=6 i f(0)=f(−6)=		⇒p=		= −3 i f(0)=		i W(−3,6)
	2		2		2

	3
to		=a(0+3)2+6 ⇒ 18a= −9 ⇒ a=−1/2
	2

28/ Kąt ABC dopisany |∡ABC|=β ⇒ |∡CRB|=2β zatem w trapezie prostokątnym ABRP α+2β=180^o ⇒ teza α=180^o−2β c.n.w

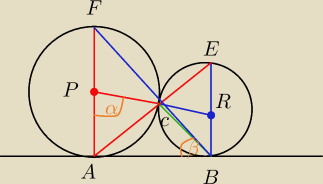
StrasznyNieogar: Trochę inna droga, ale sprawdzcie czy nie mam błedu, proszę Kąt CBR = 90 − β = kąt BCR (Bo trójkąt równoramienny) Kąt PCF również 90 − β (wierzchołkowe) Kąt ACF ma 90 stopni, bo trójkąt oparty na średnicy więckąt ACP = 90 − (90 − β) = β kąt ACP = kąt PCA 180 = 2β + α α = 180 − 2β All right?

Tangens: wg mnie źle

StrasznyNieogar: Czemu?

StrasznyNieogar: Może uzasadnisz?

Max: StrasznyNieogar: Po pierwsze, kąt ACP = kąt PAC, ale to drobny błąd. Po drugie, dodałeś punkty F i E i dorysowałeś odcinek FC i EC. Napisałeś, że kąt PCF ma miarę 90−B bo jest to kąt wierzchołkowy z kątem BCR. Ale trzeba uzasadnić, że powstały punkt F jest współliniowy z punktami A i P, bo tylko wtedy powstanie trójkąt, którego przeciwprostokątna to średnica, i tylko wtedy możemy wnioskować w następnym kroku, że kąt ACF jest kątem prostym.

StrasznyNieogar: Czyli 0 pkt?

StrasznyNieogar: "Po pierwsze, kąt ACP = kąt PAC, ale to drobny błąd" Jak to?

StrasznyNieogar: I jak można było to uzasadnić ze są współliniowe.?

Max: Napisałeś, że kąt ACP = kąt PCA. To prawda, ale nie wyciągniemy tego zadnych wniosków. To tak jakbyś napisał, że długość odcinka równa się długości odcinka |AB| = |BA|. Masło maślane. Przyrównujesz ten sam kąt. Poprawiłem Cię, bo miałeś chyba na myśli, że kąt ACP = kąt CAP, bo trójkąt ACP jest równoramienny. Spójrz jeszcze raz na swoje oznaczenia

Max: Zgadzasz się, że gdyby F nie był współliniowy z A i P, to wtedy nie mielibyśmy trójkąta i cały dowód leży, prawda? Tak, te punkty będą współliniowe, ale to wcale nie jest oczywiste i trzeba to uzasadnić. Pytasz jak? Nie wiem, mózg mi teraz nie funkcjonuje może ktoś inny się wypowie?

Max: Nie wiem czy 0 punktów, to zależy od klucza i sprawdzającego. Szczerze mówiąc, jest to ciężki przypadek, i gdybym oceniał tę maturę, to musiałbym się z kimś skonsultować co to ilości przyznanych punktów, oczywiście o ile wątpliwości nie byłyby rozwiane w kluczu. Gdybym miał Cię ocenić osobiście, nie trzymając się zasad CKE, to dałbym co najmniej 1 punkt

StrasznyNieogar: Max rzeczywiacie z tym kątem masło maślane, ale na maturze jestem pewien, że napisałem inaczej, dobrze. Może się zlituje egzaminator za to, że spróbowałem innego sposobu. Pomyślę jak udowodnić wspoliniowosc ale szczerze nie mam pomysłu

StrasznyNieogar: Tak tylko mowie z tą litością. Żeby nikt się nie przyczepił Life is brutal

Max: Takim nastawieniem przywracasz mi wiarę w licealistów..

Kaspian: Super bedzie max jeszcze rozszerzenie

matilc: hmm.... chciałbym zapytać Was o zadanko z ostrosłupem, bo (niestety) przyjąłem, że ten ostrosłup ma 2 sciany takie same, a 3 inną i wynik w przyblizeniu ( po wklepaniu w kalkulator) wyszedł mi tylko/aż o 0,1 większy. Oczywiście tok rozumowania dla mojego sposobu rozwiązania był poprawny( za dużo zadań z roszerzenia zrobiłem i zastosowałem przypadek, którego tam nie było. Czy jakieś punkty za to dostanę Przez to zadanie prawdopodobnie nie uzyskam 100%, więc jestem mega wkurzony

Kaspian: jakies punkty napewno dostaniesz za to zadanie na podstawie są mało surowi

matilc: to okej, chociaż tyle, zobaczymy w czerwcu( w sumie to już praktycznie lipiec)