Odcinki w trójkącie. Izma: W trójkącie równoramiennym ostrokątnym ABC mamy dane |AC | = |BC | = b oraz |∡ACB | = α. Z wierzchołka B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, przecinającą bok AC w punkcie D. Oblicz długość odcinka BD.

Eta: https://www.zadania.info/9092733

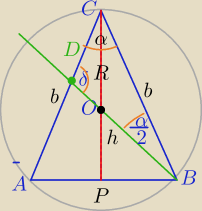
Mila: ΔABC− Δrównoramienny ostrokątny⇔ środek okręgu opisanego na tym trójkącie leży wewnątrz Δ na wysokości wychodzącej z wierzchołka między ramionami. ΔCOB− Δrównoramienny

	α		3
δ=180−(α+		)=180−		α
	2		2

Z tw. sinusów w ΔCDB:

DB		b
	=		⇔
sinα		3   sin(180− α)   2

	b*sinα
|DB|=
	sin32α

==================

Eta: