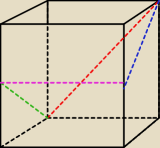
Stereometria Michał: Oblicz pole przekroju sześcianu o krawędzi a płaszczyzną zawierającą przekątną jednej ściany i środki dwóch krawędzi przeciwległej ściany. Próbowałem to narysować, ale wygląda to trochę bezsensownie.

Jerzy: Wymaż fioletową i zieloną. Niebieską przciąg teraz do środka dolnej frontowej krawędzi i do tylnego lewego wierzchołka.

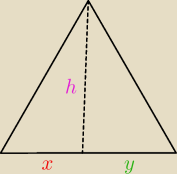
Michał: Przy okazji mam jeszcze drugie zadanie, a mianowicie: Uzasadnij wzór na pole trójkąta:

	h2 * sin (α + β)
P =
	2 * sin α * sin β

gdzie α i β są miarami kątów trójkąta przyległych do boku, na który opuszczono wysokość o długości h. Wysokość h dzieli podstawę na nierówne części x i y, tak że a = x + y Wyprowadzam wzór na pole trójkąta:

	h2 * sin (α + β)
Teza: P = 1/2 * a * h =
	2 * sin α * sin β

Po skróceniu:

	h * sin(α + β)
Teza: a =
	sin α * sin β

x = h / tg α ; y = h / tg β

	h * (tg α + tg β)
a = x + y =
	tg α * tg β

Co powinienem zrobić dalej, aby dojść do wymaganej postaci a?

Jerzy: W przekroju dostajesz trapez równoramienny.

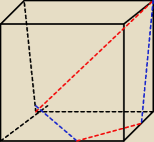
Michał: Przepraszam za rysunek. Chodzi o coś takiego?

Jerzy: Początek niebieskiej zostaw tak, jak była.

Michał:

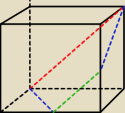
	1
I wtedy niebieskie to c, gdzie c2 = (		a)2 + a2?
	2

Jerzy: Tak.

Michał:

	3√2a
Czyli boki to a√2/3, a√5/2, a√2, a√5/2. h =		, co daje pole P =
	4

	9a2
		.
	8

Dzięki wielkie. Jeśli jeszcze mógłbym prosić o pomoc w drugim zadaniu z wykazaniem wzoru.

mamiko:

	1		1
ten zielony to d2=(		a)2+(		a)2
	2		2

	a√2
d=
	2

Michał: Tak. Źle przepisałem.

Mila: Wybieraj przekątną, aby łatwo było narysować przekrój. np. przekątna górnej podstawy.

plama:

	h(tgα + tgβ)		h*tgα		h*tgβ
dokończę to, co zacząłeś		=		+
	tgα*tgβ		tgα*tgβ		tgα*tgβ

plama: skracają się tangensy i dalej podstawiasz tgα h/x a pod tgβ podstawiasz h/y i masz bok a

plama: aaa bo już podstawiles to bez sensu co zrobiłem XD

Michał: Ale do tego momentu było dobrze?

Mila:

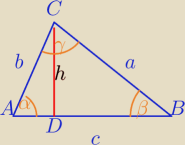
	1
PΔABC=		*a*b*sin(180−(α+β))
	2

W ΔCDB:

	h		h
sinβ=		⇔a=
	a		sinβ

W ΔCDA:

	h		h
sinα=		⇔b=
	b		sinα

	1		h		h
PΔABC=		*		*		sin(180−(α+β))⇔
	2		sinβ		sinα

	h2*sin(α+β)
PΔ=
	2sinα*sinβ

========================