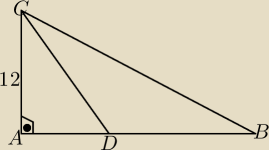
 W trójkącie ABC o polu 108 i AC=12
Na boku AB zaznaczono punkt D tak że BD=CD
Oblicz pole trójkąta BDC i długość wysokości tego trójkąta opuszczoną z wierzchołka D
na bok BC
W trójkącie ABC o polu 108 i AC=12
Na boku AB zaznaczono punkt D tak że BD=CD
Oblicz pole trójkąta BDC i długość wysokości tego trójkąta opuszczoną z wierzchołka D
na bok BC
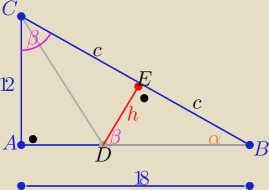 P(ABC)=6*|AB| =108 ⇒ |AB|=18 to 2c=√122+182= 6√13 , c= 3√13
z podobieństwa trójkątów ABC i BDE z cechy (kkk)
P(ABC)=6*|AB| =108 ⇒ |AB|=18 to 2c=√122+182= 6√13 , c= 3√13
z podobieństwa trójkątów ABC i BDE z cechy (kkk)
| 12 | ||
=18}{c} ⇒ h= 2√13 | ||
| h |