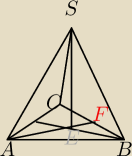
Zadanie optymalizacyjne Natalia: Znajdz wysokosc i dlugosc krawedzi podstawy ostroslupa prawidlowego trojkatnego o najmniejszym polu powierzchni przy danej objętości a. Próbowałam zrobić to tak: H−wys. ostrosłupa h_ś−wysokość ściany bocznej h−wysokość podstawy x−długość krawędzi podstawy

	x2√3
V=		*H
	4

	x2√3
a=		*H
	4

	4a√3
H=
	x2

	3		x2√3
Pc=		*x*hś+
	2		4

z podstawy ABC

	1		x√3		1		x√3
|EF|:		h=		*		=
	3		2		3		6

|EF|²+H²= h_ś²

	x4+48a√3
hś= P{		}
	12x2

I wychodzi mi takie coś:

	3		x4+48a√3		x2√3
P(x)=		*x*P{		}+
	2		12x2		4

Jak zrobić poprawnie to zadanie ?

Kacper: Skąd to zadanie? Na pewno taka treść?

Natalia: Nie wiem czy na pewno taka treść, bo zadanie mam "z drugiej ręki"

Kacper: To lepiej nie ryzykować, bo to może trefny towar