Oblicz objętość ostrosłupa trójkątnego
sty:
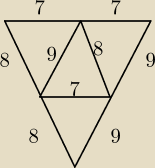
Oto szkic siatki ostrosłupa trójkątnego. Oblicz jego objętość.
3 maj 14:37
sty: :C
3 maj 16:19
Poloniusz:
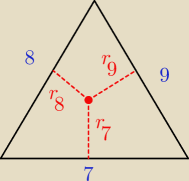
| | √(9+7+8)(9+7−8)(9−7+8)(−9+7+8) | |
P=Pp= |
| =12√5 |
| | 4 | |
h
7 − wysokość padająca na bok 7, itd.
| | 24√5 | | 24√5 | | 24√5 | |
h7= |
| , h8= |
| , h9= |
| |
| | 7 | | 8 | | 9 | |
| 1 | | 1 | | 1 | |
| *7*r7+ |
| *8*r8+ |
| *9*r9=12√5 |
| 2 | | 2 | | 2 | |
7r
7+8r
8+9r
9=24
√5
H − wysokość ostrosłupa
H
2+r
i2=h
i2 gdzie i∊{7; 8; 9}
7
√h72−H2+8
√h82−H2+9
√h92−H2=24
√5
dostajemy skomplikowane lecz do policzenia równanie z którego możemy wyznaczyć wysokość
ostrosłupa
3 maj 16:20
Poloniusz: dziękuję, bo nikt mi za to inny nie podziękuje
3 maj 17:04
Mila:
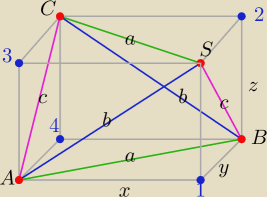
a=9, b=8, c=7
Jakoś autor nie jest zainteresowany.
Może ma odpowiedź do zadania?
Umieszczamy czworościan w prostopadłościanie o wymiarach x,y,z
Objętość ostrosłupa:
| | 1 | | 1 | |
Vo=x*y*z−4* |
| *( |
| x*y*z) |
| | 3 | | 2 | |
od objętości prostopadłościanu odejmujemy objętość 4 naroży.
x
2+y
2=81
x
2+z
2=64
y
2+z
2=49
−−−−−−−−−−−−−
y
2−z
2=17
y
2+z
2=49
2y
2=66⇔y
2=33⇔y=
√33
33+z
2=49⇔z
2=16⇔z=4
x
2+16=64⇔x
2=48⇔x=4
√3
| | 1 | |
Vo=4√3*4*√33−4* |
| *4√3*4*√33⇔ |
| | 6 | |
V
o=48
√11−32
√11
V
o=16
√11
===========
3 maj 20:42
Mila:
Spodek wysokości ostrosłupa znajduje w ortocentrum wyjściowego trójkąta.
3 maj 22:06
Poloniusz: Według mojego sposobu oraz programu wolfram alpha otrzymałem ten sam wynik
dziękuję za pani słowa
3 maj 23:45
Mila:
Policzę też Twoim sposobem ( na piechotę, bo chcę zobaczyć pracochłonność.
Zdajesz maturę w tym roku?
3 maj 23:59