optymalizacja PrzyszlyMakler: W parabole y=6−x2 wpisano prostokąt, w taki sposób, że dwa jego wierzchołki leżą na osi OX, a dwa pozostałe na paraboli (patrz rysunek). Uzasadnij, że pole każdego takiego prostokąta jest nie większe od 8√2 Na rysunku A(−m,0) B(m,0) Dziedzina (miejsca zerowe) m∊(−√6;√6) długośc podstawy a = |2m| b= |−m² +6| Czyli funkcja wyrażająca pole f(m)= |−m² +6|* |2m|= |m−√6||m+√6|*|2m| I widziałem jak inni ludzie rozwiązywali to bez modułów. Dlaczego tak można? Czy tak można? Dlaczego "można opuścic modulu?"

Omikron: Ustalasz sobie m∊(0,√6) albo (−√6,0) Wszystko wtedy dobrze wyjdzie bo z drugiej strony masz − m. Trzeba tak zrobić żeby pozbyć się modułu, z modułu pochodnej nie obliczysz.

PrzyszlyMakler: Czylli trzeba rozpatrzyć dwa przypadki? A co z '0'? Nie uwzględniamy w żadnej dziediznie?

Omikron: Jeżeli by m równało się zero to to nie byłby prostokąt. Nie dwa przypadki, wybierasz dowolny i dla niego zdejmujesz moduł odpowiednio.

PrzyszlyMakler: m∊(0;√6) −(m−√6)(m+√6)*2m = −(m²−6)2m = −2m³+12m m∊(−√6; 0) −2m³+12m więc w sumie wyjdzie to samo i tylle? i teraz tylko pochodna− też z uwzględnieniem przypadku?

Omikron: Nie wyjdzie ta sama pochodna, w drugim przypadku jeszcze 2m zdejmujesz że zmiaą znaku. Tak, dalej liczysz pochodną z uwzględnieniem dziedziny, ostatecznie wyjdzie na to samo.

PrzyszlyMakler: Czyli− rozpatrzam dwa przypadki. A co by było, gdyby się nie pokryły?

Omikron: Nie, wybierasz jeden z nich. Ostatecznie pole w obu wyjdzie zawsze takie samo. Jeżeli wierzchołek z prawej strony masz (m, 0), to wiadomo że to m jest dodatnie. Wtedy − m jest ujemne. Jeżeli oznaczylbyś wierzchołek z prawej jako − m to to musiałoby być dodatnie, więc m ujemne.

PrzyszlyMakler: trochę rozumiem, jednak wciąż przez mgłę.. to po co nam moduły? opuścić je od razu skoro i tak zawsze wyjdzie to samo

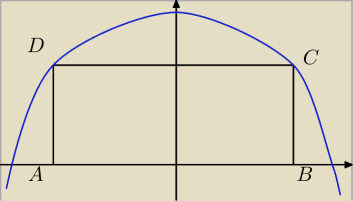
Omikron: A(−m,0) B(m,0) C(m,6−m²) D(−m,6−m²) Z rysunku widać, że m znajduje się po prawej stronie wykresu, jest w takim razie dodatnie. Gdybyśmy oznaczyli A(m,0), to B(−m,0) itd. Wtedy m byłoby ujemne (możemy wybrać dowolnie). Szukamy pola prostokąta. P=|2m|*|−m²+6|=2|m|*|√6−m|*|√6+m| Ponieważ m jest dodatnie i −m²+6 dodatnie, to wychodzi na to, że m∊(0,√6) Zdejmujemy odpowiednio moduł. P=2m*(√6+m)(√6−m)=2m*(6−m²)=2(−m³+6m) Niech f(m)=2(−m³+6m) D=(0,√6) f'(m)=2(−3m²+6)=6(−m²+2)=−6(m−√2)(m+√2) f'(m)=0 ⇔ m=√2 (przy podanej dziedzinie) f'(m)<0 ⇔ m∊(√2,√6) f'(m)>0 ⇔ m∊(0,√2) Wynika z tego, że w punkcie m=√2 jest maksimum lokalne, a przy podanej dziedzinie i monotoniczności jest to wartość największa. f(√2)=2(−2√2+6√2)=8√2 Odp. Uzasadniłem, że maksymalne pole takiego prostokąta wynosi 8√2.

Omikron: Możesz moduły opuścić po podaniu założenia dla m, czyli wartości jakie uznajesz, że może przyjmować.

PrzyszlyMakler: Ok, dziękuję. Ładnie rozpisane .

Omikron: To jest taka taka pełna formułka którą jeszcze z przygotowania do matury pamiętam