okrąg opisany na czworokącie
xxx: Na czworokącie ABCD można opisać okrąg.Dwusieczna kąta przy wierzchołku A i dwusieczna kąta
przy wierzchołu B przecinają się w punkcie E leżącym na boku CD. Na boku CD wybrano punkt F
taki, że |DA| = |DF|.
Wykaż, że |BC| = |CF|.
1 maj 23:07
xxx: podbijam
1 maj 23:16
zadanko:
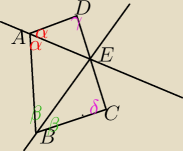
1 maj 23:25
zadanko: Z założenia 2α+δ=180 oraz 2β+γ=180
1 maj 23:27
xxx: No tak − i?
2 maj 06:23
xxx: czy ktoś jest w stanie to szybko rozwiązać?
2 maj 15:08
Mila:
Masz błąd w treści.
Punkt F obrano na boku ?
2 maj 16:24
xxx: No właśnie mnie też to dziwi, ale zarówno punkt E (pkt przecięcia się dwujęzyczne kątów przy
wierzchołkach A i B) i F leżą na boku CD
2 maj 16:37
g:
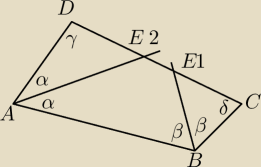
Z treścią wszystko jest w porządku. Punkt F jest tylko dla zmyłki. Chodzi o wykazanie, że
AD+BC=CD. To wygląda na trudne. W szczególności nie wiem jak wykorzystać warunek, że
dwusieczne przecinają się w punkcie leżącym na CD. Dlatego, żeby ominąć tą trudność,
próbowałem wykazać trochę ogólniejszy przypadek, że czworokąt jest dowolny i dwusieczne
przecinają się z CD w różnych punktach E1 i E2. Wtedy trzeba by udowodnić, że
AD+BC=CE1+E2D. Gdyby to się udało, to zadanie było by też rozwiązane.
Ale tego też jeszcze nie mam.
2 maj 17:01
g: ... czworokąt dowolny, ale wpisany w okrąg.
2 maj 17:04
Mila:
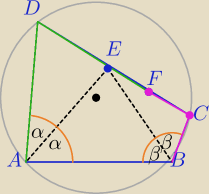
2 maj 17:22
xxx: Czyli − jak rozumiem − zadanie sprowadza się do wykazania, że pkt E = F (pokrywa się)?
2 maj 18:07
Mila:
|FC|=BC| masz wykazać, czyli tak jak napisał g:
|AD|+|BC|=|DC|
myślę jak to zrobić.
Skąd masz to zadanie?
2 maj 18:11
xxx: Zadanie maturalne z jakiegoś arkusza próbnego.
Małem na myśli w poprzednim poście, że chyba do tego to się sprowadzi−)
2 maj 18:14
xxx: A może i nie

2 maj 18:15
tobiaszek: Czy ma ktoś pomysł na to zadanie?
11 lis 19:17
chichi:
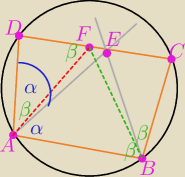
|∡ABE|=|∡EBC|=β
|∡DAE|=|∡EAB|=α
1) Na czworokącie ABCD można opisać okrąg, zatem |∡ADF|=180°−2α
2) |AD|=|DF| ⇒ |∡DAF|=|∡DFA|=β
3) |∡AFC|=180°−β
4) Na czworokącie ABEF można opisać okrąg, ponieważ |∡ABE|+|∡AFC|=180°−β+β=180°
5) ∠EAB (wpisany oparty na łuku EB)
6) ∠EFB (wpisany oparty na łuku EB)
7) Z (6) i (7) wnioskujemy, że |∡EAB|=|∡CFB|=α
8) |∡ECB|=180°−2α
9) Z ΔFBC: 180°−2α+α+|∡FBC|=180° ⇒ |∡FBC|=α
10) |∡CFB|=|∡FBC| ⇒ |CF|=|BC|
Q.E.D.
11 lis 19:56
chichi: Mała poprawka w (1) |∡ADF|=180°−2β oczywiście

11 lis 19:58
tobiaszek: Muszę poddać głębszej analizie to co Pan/Pani napisał/a, tak czy inaczej ogromne DZIĘKUJĘ.
11 lis 20:09
Eta:

11 lis 20:12
chichi: Nieeee, tylko nie Pan

mam dopiero 20 lat. Ależ proszę Cię bardzo, w razie pytań pisz

11 lis 20:12
chichi: @
Eta A ty co tak skaczesz po postach i wstawiasz emotikony

11 lis 20:13
Eta:
Z nudów

11 lis 20:14
BiałyMyjec: @chichi skąd wiesz że |∡DAF| i |∡DFA| równają się β?
punkt (2)
1 mar 18:43
BiałyMyjec: Ja rozumiem, że ten trójkąt jest równoramienny, ale czemu akurat β?
1 mar 18:45
chichi:
Napisalem, że na czworokacie ABCD można opisać okrąg, a to prosty wniosek |∡ABC|+|∡ADC|=180o,
ale my wiemy, że |∡ABC|=2β, zatem mamy 2β+|∡ADC|=180o ⇒ |∡ADC|=180o−2β ⇒|∡DAF|=|∡DFA|=β
1 mar 22:57

 Z treścią wszystko jest w porządku. Punkt F jest tylko dla zmyłki. Chodzi o wykazanie, że
AD+BC=CD. To wygląda na trudne. W szczególności nie wiem jak wykorzystać warunek, że
dwusieczne przecinają się w punkcie leżącym na CD. Dlatego, żeby ominąć tą trudność,
próbowałem wykazać trochę ogólniejszy przypadek, że czworokąt jest dowolny i dwusieczne
przecinają się z CD w różnych punktach E1 i E2. Wtedy trzeba by udowodnić, że
AD+BC=CE1+E2D. Gdyby to się udało, to zadanie było by też rozwiązane.
Ale tego też jeszcze nie mam.
Z treścią wszystko jest w porządku. Punkt F jest tylko dla zmyłki. Chodzi o wykazanie, że
AD+BC=CD. To wygląda na trudne. W szczególności nie wiem jak wykorzystać warunek, że
dwusieczne przecinają się w punkcie leżącym na CD. Dlatego, żeby ominąć tą trudność,
próbowałem wykazać trochę ogólniejszy przypadek, że czworokąt jest dowolny i dwusieczne
przecinają się z CD w różnych punktach E1 i E2. Wtedy trzeba by udowodnić, że
AD+BC=CE1+E2D. Gdyby to się udało, to zadanie było by też rozwiązane.
Ale tego też jeszcze nie mam.


 |∡ABE|=|∡EBC|=β
|∡DAE|=|∡EAB|=α
1) Na czworokącie ABCD można opisać okrąg, zatem |∡ADF|=180°−2α
2) |AD|=|DF| ⇒ |∡DAF|=|∡DFA|=β
3) |∡AFC|=180°−β
4) Na czworokącie ABEF można opisać okrąg, ponieważ |∡ABE|+|∡AFC|=180°−β+β=180°
5) ∠EAB (wpisany oparty na łuku EB)
6) ∠EFB (wpisany oparty na łuku EB)
7) Z (6) i (7) wnioskujemy, że |∡EAB|=|∡CFB|=α
8) |∡ECB|=180°−2α
9) Z ΔFBC: 180°−2α+α+|∡FBC|=180° ⇒ |∡FBC|=α
10) |∡CFB|=|∡FBC| ⇒ |CF|=|BC|
Q.E.D.
|∡ABE|=|∡EBC|=β
|∡DAE|=|∡EAB|=α
1) Na czworokącie ABCD można opisać okrąg, zatem |∡ADF|=180°−2α
2) |AD|=|DF| ⇒ |∡DAF|=|∡DFA|=β
3) |∡AFC|=180°−β
4) Na czworokącie ABEF można opisać okrąg, ponieważ |∡ABE|+|∡AFC|=180°−β+β=180°
5) ∠EAB (wpisany oparty na łuku EB)
6) ∠EFB (wpisany oparty na łuku EB)
7) Z (6) i (7) wnioskujemy, że |∡EAB|=|∡CFB|=α
8) |∡ECB|=180°−2α
9) Z ΔFBC: 180°−2α+α+|∡FBC|=180° ⇒ |∡FBC|=α
10) |∡CFB|=|∡FBC| ⇒ |CF|=|BC|
Q.E.D.


 mam dopiero 20 lat. Ależ proszę Cię bardzo, w razie pytań pisz
mam dopiero 20 lat. Ależ proszę Cię bardzo, w razie pytań pisz 

