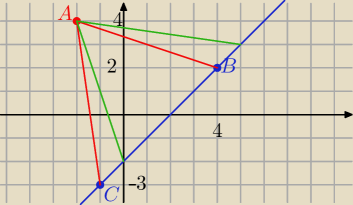
Oblicz współrzędne wierzchołka C. Julka: Punkt A(−2;4) jest jednym z wierzchołków trójkąta równoramiennego ABC, którego pole jest równe 20 AC=BC Bok BC jest zawarty w prostej o równaniu y=x−2. Oblicz współrzędne wierzchołka C.

Janek191: A = ( − 2, 4) B = ( a, a − 2) C = ( b, b − 2) x − y − 2 = 0 h − odległość A od danej prostej.

	I 1*(−2) −1*(4) − 2 I		8
h =		=		= 4√2
	√2		√2

Ma być 0,5 I BC I*h = 20 / *2 I BC I* 4 √2 = 40 I BC I = 5√2 I AC I = I BC I ⇒ I AC I² = I BC I² ( b + 2)² + ( b − 6)² = ) 5√2)² b² + 4 b + 4 + b² − 12 b + 36 = 50 2 b² − 8 b − 10 = 0 / : 2 b² − 4 b − 5 = 0 ( b − 5)*( b + 1) = 0 b = − 1 lub b = 5 więc C = ( − 1, − 3) lub C = ( 5, 3) B = ( a, a − 2) I BC I² = I A C I² 50 = (a + 1)² = ( a + 1)² = 2*( a² +2 a + 1) =2 a² + 4 a + 2 2 a² + 4 a − 48 = 0 a² +2 a − 24 = 0 Δ = 4 − 4*(−24) = 100 √Δ = 10

	− 2 − 10
a =		= − 6 lub a = 4
	2

B = ( 4, 2) ========

Janek191: