Prawdopodobieństwo warunkowe Gustaw: Ze zbioru X = {x: x ∊ C i |x−1| ≤ 4} losujemy dwa razy (ze zwracaniem) po jednej liczbie. Oznaczmy te liczby w kolejności losowania a oraz b. Oblicz prawdopodobieństwo zdarzenia, że para liczb (a, b) jest rozwiązaniem nierówności y−x+2>0, jeżeli wiadomo, że liczba b jest nieujemna.

dociekliwy: Potrafisz określić zbiór X ?

Sigma: Zbiór x : odległość od 1 jest mniejsza lub równa od 4 czyli x∊<−3,5> przy czym uwzględniamy tylko liczby całkowite

Gustaw: Tak, zbiór to bez problemu, bardziej mnie dalsza część interesuje.

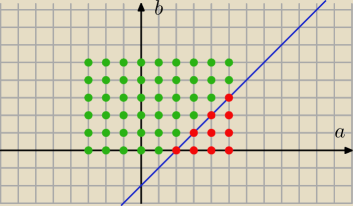
Pytający: a∊{−3,−2,−1,0,1,2,3,4,5} b∊{0,1,2,3,4,5} |Ω|=9*6=54 Pary (a,b) nie spełniające nierówności b>a−2: (5,3) (5,2),(4,2) (5,1),(4,1)(3,1) (5,0),(4,0)(3,0),(2,0)

	54−10		22
P=		=
	54		27

Pytający:

dociekliwy: |Ωl= 9*9