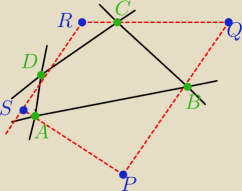
 Dany jest czworokąt ABCD. Punkty P,Q,R,S są punktami przecięcia dwusiecznych jego
kątów zewnętrznych. Udowodnij, że na czworokącie PQRS można opisać okrąg.
Zadanie z z przykładowej matury rozszerzonej. Czy ktoś ma jakiś pomysł na rozwiązanie?
Dany jest czworokąt ABCD. Punkty P,Q,R,S są punktami przecięcia dwusiecznych jego
kątów zewnętrznych. Udowodnij, że na czworokącie PQRS można opisać okrąg.
Zadanie z z przykładowej matury rozszerzonej. Czy ktoś ma jakiś pomysł na rozwiązanie?

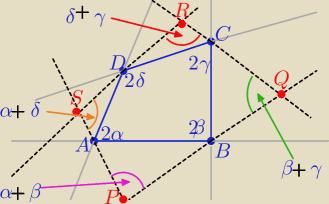 2α+2β+2γ+2δ=360o to α+β+γ+δ=180o
W czworokącie PQRS sumy kątów przeciwległych to
α+δ+β+γ =180o i α+β+δ+γ =180o
wniosek...... daje tezę
2α+2β+2γ+2δ=360o to α+β+γ+δ=180o
W czworokącie PQRS sumy kątów przeciwległych to
α+δ+β+γ =180o i α+β+δ+γ =180o
wniosek...... daje tezę

