zad PrzyszlyMakler: Punkty A i B są punktami współlnymi prostej x + y −5= 0 oraz okręgu (x−2)² + (y−1)² = 20 na okręgu wyznacz taki punkt C aby pole trójkąta ABC było jak największe. A(0,5) B(6,−1) Prosta AB: y=−x+5 Prosta zawierająca wierzchołek C = y=x + b Jak udowodnić, że aby pole było największe wysokość musi przechodzic przez środek okręgu?

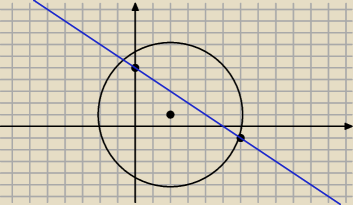
5-latek: Cos nie tak

PrzyszlyMakler: ale promień narysowanego przez Ciebie okręgu ma długość 6, a tego w zadaniu ma ok. 4,5

5-latek: No to ktorys punkt nie pasuje

PrzyszlyMakler: (x−2)²+(−x +5 − 1)² = 20 x² −4x + 4 (−x +4)² = 20 x² −4x + 4 +16−8x +x² = 20 2x² −12x=0 2x(x−6) = 0 x= 0 v x=6 y=−x + 5 A(0,5) B (6, −1) Nie wiem co Ci nie pasuje, moim zdaniem wszystko jest dobrze.

PrzyszlyMakler: #pomocy. Wydaje mi sie logiczne, że to musi przechodzic przez środek, jednak chciałbym "fachowego uzasadnienia"

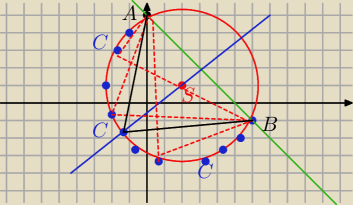
5-latek: Zrobilem inny rysunek(inne kratki ) i wyszlo ok tam tez byl r≈4,5 bo S= (2,1) a nie S=(0,0) Jest takie twirdzenie Prostopadla wykreslona ze srodka okregu do cieciwy dzieli ja na polowy Niebieskie kropki obrazuja polozenie punktu C Zeby to pole tego trojkata bylo najwiekszse to wysokosc musi byc najiewksza przy danej podstawie Kiedy ta wysokosc bedzie najwieksza ? Kiedy cieciwa bedzie podzielona na polowy i dostaniemy trojkat rownoramienny (tutaj

5-latek: Moze jeszce spojrzy Mila Po zdrawiam lub Eta

PrzyszlyMakler: ok, dzięki

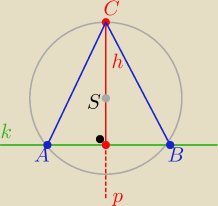
Eta: Nie ma potrzeby wyznaczania współrzędnych punktów A i B bo: Pole trójkąta jest największe przy danej podstawie AB wtedy gdy długość wysokości h_AB jest największa a to ma miejsce gdy wysokość zawiera się w prostej p prostopadłej do k i przechodzącej przez środek S okręgu Szukany punkt C leży właśnie na tej prostej p S(2, 1) k: y=−x+5 to p : y=(x−2)+1 ⇒ y=x−1 rozwiąż układ równań prostej p z okręgiem otrzymasz dwa punkty C ( jeden odrzuć , bo nie spełnia warunków zadania ...................... powodzenia Odp: C(2−√10,1−√10) ( o ile się nie pomyliłam w obliczeniach ============

PrzyszlyMakler: Eto! Ale ja to wiem, ja chciałem dowód, że musi przechodzić przez środek okręgu . Pozdrawiam.

Eta: Czytaj początek wpisu............ ( masz uzasadnienie!