dla eksperta
typek: Rozważmy czworokąt wypukły ABCD. Niech E i F oznaczają kolejno punkty styczności okręgów
wpisanych w trójkąty ABD oraz BCD z przekątną BD. Wykaż, że jeśli E = F, to w czworokąt ABCD
można wpisać okrąg.
29 kwi 19:14
matura 2017:
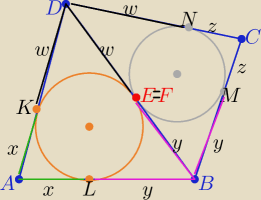
W odwrotną stronę
Jeżeli E=F to przekształcając równoważnie otrzymuję
z twierdzenia o odcinkach stycznych:
|AL|=|AK|=x |BL|=BM|=y ........ itd
zatem: sumy długości boków przeciwległych są równe
|AD|+|BC|= x+w+y+z i |AB|+|DC|= x+y+w+z
czyli w taki czworokąt można wpisać okrąg
więc punkty E i F pokrywają się co zgadza się z założeniem

29 kwi 20:08
typek: dzięki bardzo
29 kwi 20:30
matura 2017:

29 kwi 20:34
 W odwrotną stronę
Jeżeli E=F to przekształcając równoważnie otrzymuję
z twierdzenia o odcinkach stycznych:
|AL|=|AK|=x |BL|=BM|=y ........ itd
zatem: sumy długości boków przeciwległych są równe
|AD|+|BC|= x+w+y+z i |AB|+|DC|= x+y+w+z
czyli w taki czworokąt można wpisać okrąg
więc punkty E i F pokrywają się co zgadza się z założeniem
W odwrotną stronę
Jeżeli E=F to przekształcając równoważnie otrzymuję
z twierdzenia o odcinkach stycznych:
|AL|=|AK|=x |BL|=BM|=y ........ itd
zatem: sumy długości boków przeciwległych są równe
|AD|+|BC|= x+w+y+z i |AB|+|DC|= x+y+w+z
czyli w taki czworokąt można wpisać okrąg
więc punkty E i F pokrywają się co zgadza się z założeniem

