Prostopadłościan, przekrój oskigw: Przekątna prostopadłościanu o podstawie kwadratowej ma długość 20√5 i jest nachylona do płaszczyzny podstawy tego prostopadlosciany pod kątem α takim, że tgα=3. Prostopadłościan przecięto płaszczyzna przechodzącą przez przekątna podstawy i nachylona do niej pod kątem 30 stopni, Oblicz pole otrzymanego przekroju. Obliczyłem krawędź podstawy a=10, ale nie wiem jak sie zabrać za przekrój.

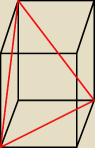
oskigw: Tak będzie wyglądał przekrój?

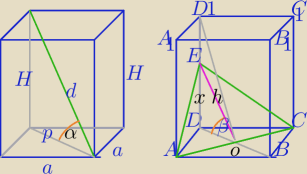
Mila: tgα=3 d=20√5

	H
1) tgα=
	p

	H
3=
	a√2

H=3a√2 d²=p²+H² (20√5)²=(a√2)²+(3a√2)²⇔400*5=2a²+18a² 400*5=20a² a=10 ===== 2) H=30√2 3) β=30^o

	√3
tg30o=
	3

	√3		x
W ΔEDO:		=
	3		5√2

	5√6
x=		<H
	3

Zatem Twój przekrój nie jest dobry. 4) W ΔEDO:

	|OD|
cosβ=
	h

	5√2
cos30o=
	h

√3		5√2
	=
2		h

licz dalej sam.