maturalne
5-latek: tylko dla maturzystow
Zadanie nr 1 Napisac rownanie krzywej bedacej zbiorem wszystkich punktow ktorych odleglosci
od okregu o rownaniu x
2+y
2=100 i punktu A=(,6,0) sa rowne
Naszkicowac te krzywa
Zadanie nr 2
Obliczyc obwod tego z trapezow rownoramiennych majacych krotsza podstawe 2a oraz ramie a
ktory ma najwiekszse pole powierzchni
zadanie nr 3
Wykazac ze jesli rownanie x
3+ax+b=0 ma pierwiastek podwojny to 4a
3+27b
2=0
Zadanie nr 4 Rozwiazac nierownosc
| cos2x | |
| <1 dla x∊(0,π) |
| cosx | |
Zadanie nr 5
Wykazac ze okrag wpisany w trojkat protokatny jest styczny do przeciwprostokatnej w punkcie
dzielacyn przeciwprostokatna na dwa odcinki ktorych iloczyn dlugosci jesr rowny
polu powierzchni tego trojkata
Zadanie nr 6 Z cyfr 1,2,3,4,5,6,7,8,9 losujemy bez zwracania trzy cyfry ukladajac je w
kolejnosci losowania w liczbe
Zakladajac ze wszystkie mozliwe do otrzymania w ten sposob liczby sa jednakowo przwdopodobne
,obliczyc prawdopodobienstwo otrzymania liczby mniejszsej od 666.
Zadanie nr 7
W ostroslupie prawidlowym czworokatnym odleglosci srodka wysokosci od krawedzi bocznej i
sciany bocznej wynosza odpowiednio a i b
Wyznaczyc objetosc ostroslupa i podac warunek rozwiazalnosci zadania
Zadanie nr 8
WYznaczyc wartosc x dla ktorych istnieje granica
| | 1 | | 2x+1 | | 2x+1)n−1 | |
lim n→∞[ |
| + |
| + .......+( |
| ] |
| | x+2 | | (x+2)2 | | (x+2)n | |
I obliczy te granice
29 kwi 16:32
5-latek: Zestaw nr 2
zadanie nr 1
Wyznaczyc wartosci parametrow mi n dla ktorych okrag o rownaniu x2+y2+mx+ny−8=0 jest
styczny do prostych o rowniach 4x−3y−18=0 i 4x−3y−12=0
zadanie nr 2
Z puntu A(1,1) wychodza dwie polproste prostopadle przecinajace osie ukladu wspolrzednych
Niech F bedzie obszarem kąta prostego wyznaczonego przez te polproste
Niech G bedzie zbiorem wszystkich punktow o obydwu wspolrzednych nieujemnych
Wyznaczyc polozenie polprostych dla ktorych pole powierzchni F∩G jest najmniejszse
Zadanie nr 3
Niech an bedzie takim ciagiem ze a1= √2 oraz an+1=( √2)log2an
CIUag bn okreslamy wzorem bn= a1*a2*......* an
Obliczyc lim n→∞bn
zadanie nr 4
Na okregu o srednicy d opisano trapez rownoramienny o podsatwaach dlugosci a i b
Wykazac ze d=√a*b
Zadanie nr 5
ROzpatrujemy zbior ciagow n−wyrazowych o wyrazach (−1),0 lub 1
Obliczyc pradopodobienstwo tego ze ze losowo wybrany ciag ma co najwyzej jeden wyraz rowny 0
i suma jego wyrazow jest rowna 0
29 kwi 16:47
matura 2017:
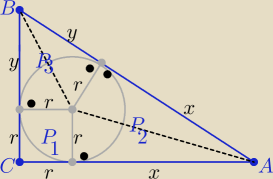
Zestaw 1 zad.5
Porządny rysunek .... ( to 3/4
sukcesu  P
P(ABC)=P
1+P
2+P
3=r
2+rx+ry
oraz z tw. Pitagorasa w ΔABC
(x+r)
2+(y+r)
2=(x+y)
2⇒ 2r
2+2rx+2ry=2xy /;2 ⇒ r
2+rx+ry=xy=
P
P=x*y
=====
c.n.w

29 kwi 17:09
5-latek: Tak samo mysle jak Pani

Pozdrawiam
29 kwi 17:17
Przyszłymakler:
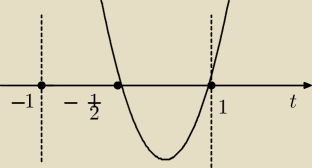
Zadanie 4.
dla x ∊(0;π)
D:cosx ≠ 0
x≠ π/2 +kpi
cosx−t t∊<−1;1>
t(2t
2−t−1) <0
Δ= 9
t1 = 1
t(2t
2−t−1) <0
t<0 dla x ∊ ({π}{2};π)
| | 1 | | 2 | |
2t2−t−1>0 dla t∊(−1;− |
| ) → dla x ∊ ( |
| π;π) |
| | 2 | | 3 | |
| | 1 | | 2 | |
2t2−t−1<0 dla t ∊(− |
| ; 1) → dla x ∊(0; |
| π) |
| | 2 | | 3 | |
iloczyn dwóch wyrażen jest ujemny, gdy jedno z nich jest ujemne, a drugie dodatnie
| | π | | 2 | |
tak się dzieje dla x∊ (0; |
| ) u( |
| π;π) |
| | 2 | | 3 | |
29 kwi 17:32
5-latek: Taka jest odpowiedz do zadania
29 kwi 17:35
Przyszłymakler: Zadanie 5.
{1,2,3,4,5,6,7,8,9}
Ω= 9*8*7
Zdarzenie przeciwne, liczba większa niż 666.
(671, 672,673,674,675,678,679) = 7
(681,682, 683,684, 685,687, 689) = 7
(691, 692, 693, 694, 695, 697, 698) = 7
na pierwszym miejscu 7 na drugim coś spośród 8 cyft, na trzecim spośród 7
1*8*7
na pierwszym miejscu 8...
1*8*7
na pierwszym miejscu 9
1*8*7
|A'| = 7+7+7+56+56+56 = 189
A = 9*8*7 − 189 = 315
| | 315 | | 105 | | 35 | |
P(A) = |
| = |
| = |
| |
| | 504 | | 168 | | 56 | |
29 kwi 17:42
Przyszłymakler: Powyższe zadanie to oczywiście zadanie 6, przepraszam
29 kwi 17:43
5-latek: | | 5 | |
Po skroceniu = |
| tak jak w odpowiedzi |
| | 8 | |
29 kwi 17:49
matura 2017:

...... dla
maklera 
29 kwi 17:54
Przyszłymakler: 6 było łatwe, 4 chciałem spróbować, bo z trygonometrią to ja tak średnio. Wieczorem może
spróbuję 7 jeszcze

Dzięki za jabłko. Twój dowód też niczego sobie

29 kwi 18:04
5-latek: Tylko czasami
matura2017 lubi dawac dwa


Z tym ze jedno jest robaczywe i musisz wybrac (tak jak kiedys
bezendu 
29 kwi 18:12
et2: matura 2017 = ETA?
29 kwi 21:53
matura 2017:

29 kwi 21:55
et2: to było zbyt oczywiste
29 kwi 22:07
Adamm: zestaw 2
zad 5
dla n=2k
|Ω|=3
2k
dla n=2k+1
|Ω|=3
2k+1
29 kwi 22:21
5-latek: Adamm
Musi mnie ktos nauczyc wstawiac skany tutaj na forum
Wtedy wstawie CI rozwiazanie tego zdania (bo jest duzo pisania
30 kwi 12:59
 Zestaw 1 zad.5
Porządny rysunek .... ( to 3/4 sukcesu
Zestaw 1 zad.5
Porządny rysunek .... ( to 3/4 sukcesu  P(ABC)=P1+P2+P3=r2+rx+ry
oraz z tw. Pitagorasa w ΔABC
(x+r)2+(y+r)2=(x+y)2⇒ 2r2+2rx+2ry=2xy /;2 ⇒ r2+rx+ry=xy=P
P=x*y
=====
c.n.w
P(ABC)=P1+P2+P3=r2+rx+ry
oraz z tw. Pitagorasa w ΔABC
(x+r)2+(y+r)2=(x+y)2⇒ 2r2+2rx+2ry=2xy /;2 ⇒ r2+rx+ry=xy=P
P=x*y
=====
c.n.w

 Pozdrawiam
Pozdrawiam
 Zadanie 4.
dla x ∊(0;π)
D:cosx ≠ 0
x≠ π/2 +kpi
Zadanie 4.
dla x ∊(0;π)
D:cosx ≠ 0
x≠ π/2 +kpi
 ...... dla maklera
...... dla maklera 
 Dzięki za jabłko. Twój dowód też niczego sobie
Dzięki za jabłko. Twój dowód też niczego sobie 

 Z tym ze jedno jest robaczywe i musisz wybrac (tak jak kiedys bezendu
Z tym ze jedno jest robaczywe i musisz wybrac (tak jak kiedys bezendu 
