kąt między płaszczyznami
za tydzień mam maturę:
Sześcian ABCDA
1B
1C
1D
1 przecięto płaszczyzną AB
1D
1 i CB
1D
1. Oblicz cosinus kąta między
tymi płaszczyznami.
Mój problem nie polega na obliczeniach, ale na zaznaczeniu tego kąta. Nie bardzo wiem jak
powinnam go widzieć.
Dzięki za każdą pomoc.
29 kwi 16:24
Mila:
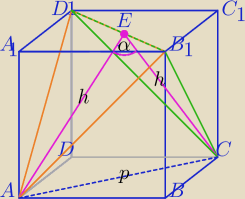
α=∡AEC
29 kwi 16:47
za tydzień mam maturę: a czym jest punkt E? tzn czy jest to środek D
1B
1 (jesli tak to dlaczego

), a moze to
wysokość poprowadzona z A?
29 kwi 17:08
Sigma: Jakie masz dane do tego zadania ?
29 kwi 17:16
Sigma: Punkt E to środek D1B1, bo pomarańczowy trójkąt jest równoramienny (ramiona przekątnymi ścian
bocznych), więc wysokość jest w połowie podstawy trójkata, czyli w połowie przekątnej górnej
podstawy. Tak mi się przynajmniej wydaje

29 kwi 17:18
za tydzień mam maturę: nie ma danych

to bardziej teoretyczne zadanie chyba, właśnie na sprawdzenie zaznaczania
kątów w przekrojach.
No w sumie, wysokość obu przekrojów będzie w połowie i to by wyjaśniało sprawę.
Dzięki

29 kwi 17:28
Mila:
ΔAD
1B
1≡ΔCB
1D
1− Δrównoboczne o boku a
√2
Z tw cosinusów:
|AC|
2=h
2+h
2−2*h*h cosα
(a
√2)
2=2h
2*(1−cosα)
=========
29 kwi 18:10
Mila:
Sigma tu wystarczy informacja, że to jest sześcian.
29 kwi 20:12
 Sześcian ABCDA1B1C1D1 przecięto płaszczyzną AB1D1 i CB1D1. Oblicz cosinus kąta między
tymi płaszczyznami.
Mój problem nie polega na obliczeniach, ale na zaznaczeniu tego kąta. Nie bardzo wiem jak
powinnam go widzieć.
Dzięki za każdą pomoc.
Sześcian ABCDA1B1C1D1 przecięto płaszczyzną AB1D1 i CB1D1. Oblicz cosinus kąta między
tymi płaszczyznami.
Mój problem nie polega na obliczeniach, ale na zaznaczeniu tego kąta. Nie bardzo wiem jak
powinnam go widzieć.
Dzięki za każdą pomoc.
 α=∡AEC
α=∡AEC
 ), a moze to
wysokość poprowadzona z A?
), a moze to
wysokość poprowadzona z A?

 to bardziej teoretyczne zadanie chyba, właśnie na sprawdzenie zaznaczania
kątów w przekrojach.
No w sumie, wysokość obu przekrojów będzie w połowie i to by wyjaśniało sprawę.
Dzięki
to bardziej teoretyczne zadanie chyba, właśnie na sprawdzenie zaznaczania
kątów w przekrojach.
No w sumie, wysokość obu przekrojów będzie w połowie i to by wyjaśniało sprawę.
Dzięki 