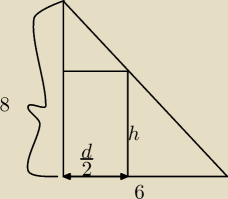
Pomoc z proporcją reltih: Dany jest stożek o promieniu podstawy 6 cm i wysokości 8 cm. W stożek ten wpisujemy prostopadłościany tak, że jedna podstawa zawiera się w podstawie stożka a wierzchołki drugiej podstawy należą do powierzchni bocznej stożka. Wiedząc, że stosunek długości krawędzi podstawy jest równy 3, oblicz wymiary tego prostopadłościanu, którego objętość jest największa. h wysokośc graniastosłupa x− długość krótszego boku podstawy d= (Pierwiastek z 10)x czy ta proprocja jest dobrze ułożona? 8−h d/2 −−− = −−−−− 8 6

reltih: proszę o odpowiedź "tak" lub "nie".

Janek191: Tak

reltih: Według mnie również ta proporcja jest dobra ale dalej wynik zły wychodzi. a kiedy użyje się takiej proprcji 8/10 = h/(6−d/2) Wychodzi dobry. Tą proprocje wziołem z tej strony: https://zadane.pl/zadanie/11518315

reltih: Więc dalej potrzebuje pomocy i wyjaśnienia.

reltih: Kto wyjaśni o co chodzi z tymi proporcjami?

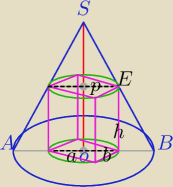
Mila: |OS|=H=8 R=|OB|=6, |OP|=h

a
	=3
b

a=3b |PE|=r

	√10
(2r)2=a2+b2⇔r=		b
	2

ΔSPE∼ΔSOB⇔

SP		H
	=
r		OB

8−h		8		2√10
	=		⇔4r=3*(8−h)⇔h=8−		b
r		6		3

	2√10
V=3b*b*(8−		b)
	3

V(b)=24b²−2√10b³ V'(b)=48b−6√10b² Ekstrema: 48b−6√10b²=0 6b*(8−√10b)=0

	4√10
b=0 lub b=
	5

V_max dla:

	4√10		12√10		8
b=		, a=		, h=
	5		5		3

=======================

reltih: Kawał dobrej roboty @Mila. Czy możesz rozwiązać to zadanie tylko ze zmienną b? b=(24−3h)/(2√10)

reltih: bo coś doliczyć się nie mogę.

reltih: ze zmienna h oczywiście.

reltih: dobra nieważne znalazłem błąd. Tyle czasu zmarnowałem na szukanie głupiego błędu. Od początku wszystko dobrze miałem. Dziękuję wszystkim za pomoc.

Mila: