Wyznaczenie punktu C Robert: Dany jest trójkąt równoramienny abc gdzie a(0,0), b(−7,11) oraz |AB|=|BC|. Punkt C leży na prostej y=2x. Znajdź współrzędne punktu C. Jak to szybko zrobić? Z góry dziękuję za pomoc.

Powracający: Zrob rysunek do zadania i przypomnij sobie wlasnosci trojkata rownoramiennego

Robert: Zrobiłem to tak, że policzyłem |AB| i |CB|. Następnie |AB|=|CB| |² itd. czy można to zrobić szybciej?

Powracający: to napisz jak zrobiles dokladnie

Robert: |AB|=√170 |CB|=√5x²−30x+170 √170=√5x²−30x+170 |² 5x²−30x+170=170 5x²−30x=0 5x(x−6)=0 x=0 v x=6 Zero odpada, bo to punkt A. y=2x y=12

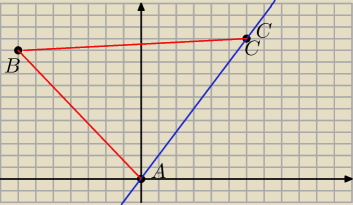
Powracający: B=(−7,11) c= (6,12) BC²= (13²+1²)= 170 BC= √170 czyli masz dobrze Tak by robil

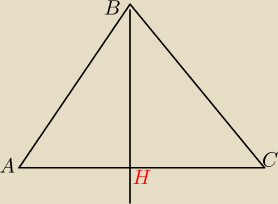
Powracający: Zadanie to mozna zrobic tez tak U nas AB i BC to ramina tego trojkata natomiast AC to podsatwa Patrz rysunek wyzej jesli napiszsemy rownanie prostej prostopadlej do y=2x i przechodzacej przez punkt B to bedzie to rownanie wysokosci tego trojata Ale wiemy ze wysokosc w trojakacie rownowamiennym wychodzaca z wierzchola pomiedzy ramionami to jednoczenie dwusieczna tego kata i srodkowa AC Wyznaczajac pukt (H) przeciecia prostych y=2x i tej prostej prostopadlej wyznaczasz srodek odcinka AC *czyli podstawy Teraz z ewzorow na wspolrzedne srodka odcinka wyznaczasz wspolrzedne punktu C Troche dluzszy sposob .