Odcinek łączący wykresy
Gah: Odcinki których jeden koniec leży na wykresie y=−2/x x≤0 a drugi na y=−(x−2)(x−2) x=R
Oblicz długość najkrótszego odcinka łączącego wykresy tych funkcji oraz podaj współrzędne
punktów dla obu wykresów
28 kwi 18:36
Janek191:
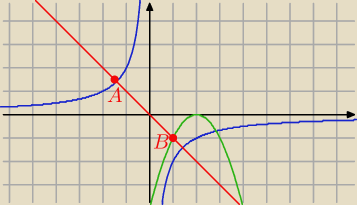
28 kwi 20:02
Gah: A obliczenia?
28 kwi 23:23
Gah: Pomoże ktoś?
29 kwi 11:32
Powracający: Po pierwsze nie odpisujesz w swoich postach . Masz to w 5 literach .
Po drugie . NIc CI nie dazda obliczenia skoro nie znasz teorii
Pytanie nr 1
| | a | |
Jakie osie symetrii ma hiperbola rownoosiowa y= |
| ? (ma dwie zapoznaj sie z tym |
| | x | |
pytanie nr 2
Kiedy odleglosc punktu od prostej jest najmniejsza ? Kiedy lezy na jakiej prostej do danej ?
Jesli to bedziesz wiedzial to po zadaniu
29 kwi 11:59
bleble:
gdybyś TY Powracający jeszcze wiedział o czym piszesz
29 kwi 14:06
Adamm: | | a | |
ja się naliczyłem 4 osi symetrii u hiperboli y= |
| |
| | x | |
29 kwi 14:10
Jerzy:
To się chyba o dwie przeliczyłeś

29 kwi 14:12
Adamm: y=0, x=0, y=x oraz y=−x
teraz mi powiedz które nadliczyłem?
29 kwi 14:12
Jerzy:
Pierwsze dwie

29 kwi 14:13
bleble:
jeszcze ciekawiej

a może nawet 15

29 kwi 14:13
Adamm: no tak

29 kwi 14:14
Jerzy:
Przecież: x = 0 i y = 0 , to asymptoty, a nie osie symetrii.
29 kwi 14:14
bleble:
a co ma wspólnego oś symetrii hiperboli z odległością jej punktów od innej krzywej?
29 kwi 14:23
Adamm: nie mam pojęcia
ty mi powiedz
29 kwi 14:24
Jerzy:
W tym zadaniu rzeczywiście rysunek Janka nic nie wnosi do rozwiązania.
29 kwi 14:26
bleble:
a jeszcze mniej komentarz Powracającego
29 kwi 14:30
Powracający: Dlazcego mniej ?
Przeciez najmniejsza jest odledlosc jesli dany punkt lezy na prostej prostopadlej do danej
jesli osia symetrii jest y=x to druga jest prostopadla i ma rownanie y=−x
Wlasnie na tej prostej musza lezec te punkty aby ich odleglosc byla najmniejsza .
| | −2 | |
Teraz policzyc punkty przecicia y== |
| z y=−x i y= (x−2)2 i y=−x i ma wspolrzedne |
| | x | |
punktow
Odlegosc tych punktow to dlugosc tegho odcinka
Hiperbola rownoosiowa ma dwie osie symetrii
Sa to dwusieczne katow miedzy jej asymptotami
Punkt ich przeciecia jest srodkiem symetrii hiperboli .
U nas os symetrii y=−x przecina hiperbole w dwoch punktach ktore sa wierzcholkami
hiperboli
Nas inretesuje tylko druga cwiartka bo x≤0 wiec punkt przeciecia bedzie mial wspolrzedne dla 2
cwiartki
To tyle .
29 kwi 14:52
Tadeusz:
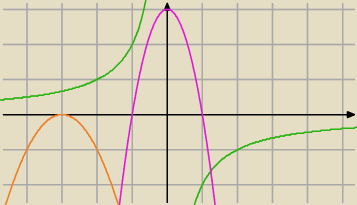
To w/g Ciebie Kol
Powracający jeden z punktów najkrótszego odcinka leży na osi
hiperboli? Pomylić się ludzka rzecz ale wmawiać to innym i sobie ...
30 kwi 10:29
jc: Być może chodzi o najkrótszy pionowy odcinek, lub o coś jeszcze innego.
W przypadku zwykłej odległości (Euklidesowej) współrzędna x−owa punktu
na hiperboli spełnia równanie x7 − 2x6+x4−4x3+2=0, x ≈ −1.24604.
30 kwi 11:05
5-latek: WItaj
Tadeusz 
Kiedys pod innym nickiem pisalem do
Kacpra zeby wyjasnil dlaczego tak a nie inaczej to mi
odpisal ze nie musi wyjasniac bo nie jest moim nauczycielem
No dobrze
PW chcial mi zasadzic kopa . Fajnie to by wygladalo jakby sie dziadki po dupie kopali

Wyjasnij mi gdzie popelniam blad myslowy
30 kwi 12:20
Jerzy:
Napisałem Ci przed chwilą przy pod innym postem.
30 kwi 12:21
5-latek: Moze tak .
Sprobuje nad tym pomyslec . jesli nic nie wymysle to poprosze o rozwiazanie .
30 kwi 12:24



 a może nawet 15
a może nawet 15

 To w/g Ciebie Kol Powracający jeden z punktów najkrótszego odcinka leży na osi
hiperboli? Pomylić się ludzka rzecz ale wmawiać to innym i sobie ...
To w/g Ciebie Kol Powracający jeden z punktów najkrótszego odcinka leży na osi
hiperboli? Pomylić się ludzka rzecz ale wmawiać to innym i sobie ...
 Kiedys pod innym nickiem pisalem do Kacpra zeby wyjasnil dlaczego tak a nie inaczej to mi
odpisal ze nie musi wyjasniac bo nie jest moim nauczycielem
No dobrze
PW chcial mi zasadzic kopa . Fajnie to by wygladalo jakby sie dziadki po dupie kopali
Kiedys pod innym nickiem pisalem do Kacpra zeby wyjasnil dlaczego tak a nie inaczej to mi
odpisal ze nie musi wyjasniac bo nie jest moim nauczycielem
No dobrze
PW chcial mi zasadzic kopa . Fajnie to by wygladalo jakby sie dziadki po dupie kopali
 Wyjasnij mi gdzie popelniam blad myslowy
Wyjasnij mi gdzie popelniam blad myslowy