bryly-ostroslup:) maturzystka:): W ostroslupie prawidlowym czworokatnym krawedz boczna tworzy z krawedzia podstawy kat α. Wyznacz kosinus kata miedzy sasiednimi scianami bocznymi. Prosze o szczegolowe rozwiazanie krok po kroku Ja sobie rozrysowalam ale szczerze mowiac nawet nie widze mozliwosci obliczenia cosβ bo nie widze w tym trojkacie kata prostego

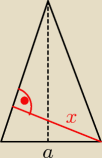
b.: być może że to nie będzie najprostsze rozwiązanie... niech bok podstawy będzie długości a wtedy krawędź boczna jest długości

	a
a/2 / (cos α) =
	2cosα

i teraz kluczowa rzecz: liczymy długość x (zob. rysunek ściany bocznej), licząc pole tej ściany bocznej na 2 sposoby:

	1		a		1		a tgα
		* x *		=		* a *
	2		2cosα		2		2

	a tgα
(		to wysokość ściany)
	2

to teraz rozważamy trójkąt, który ma 2 wierzchołki w przeciwległych wierzchołkach podstawy ostrosłupa, a trzeci wierzchołek leży na krawędzi, zob. rysunek 2 niżej ten trójkąt ma długości boków x,x, a√2 i kąt β pomiędzy bokami długości x to będzie ten nasz kąt i na koniec tw. kosinusów

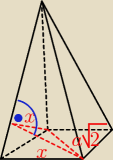b.: rysunek 2

b.: [stokrotka]