Powracający:
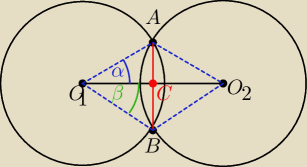
Dwa okregi przecinaja sie w punktach A i B
O
1 i O
2 to srodki tych okregow
Laczymy punkty O
1 i )
2 z punktami A i B
Otrzymamy trojakaty AO
1 O
2 i BO
1 O
2
Te trojkaty sa trojkatami przystajacymi na posdtawie echy BBB bo maja po trzy boki odpowiednio
rowne
Z przystawania tych trojkatow wynika ze ∡α=∡β
Teraz wezmy pod uwage trojkat rownoramienny AO
1 B
O
1C jest dwusieczna kata przy jego wierzcholku wiec jest prostopadle do podstawy to
AB⊥O
1O
2
W trojakcie rownoramiennym dwuieczna kata przy wierzchoklu miedzy ramionai jest jednoczenie
srodkowa i wysokoscia tego trojkata (a wysokosc jest prostopadla do podstawy
Mila:
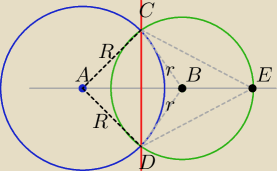
np. tak:
Punkty A, B ∊prostej AB są jednakowo odległe od końców odcinka CD [AC≡AD, BC≡BD]⇔
leżą na symetralnej tego odcinka.
Symetralna jest prostopadła do tego odcinka .
