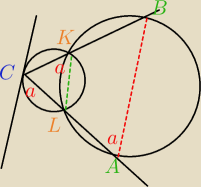
Planimetria Michał: Okręgi o₁(O₁; r₁) oraz o₂(O₂; r₂) gdzie 0 < r₁ < r₂ przecinają się w punktach K i L. Na okręgu o₁ wybrano punkt C (C ≠ K i C ≠ L) i poprowadzono styczną p do tego okręgu w punkcie C. Następnie poprowadzono półproste CK i CL, które przecięły okrąg o₂ odpowiednio w punktach A i B. Wykaż, że prosta p jest równoległa do prostej AB. Przyjmuję, że BAC to kąt α. Tylko nie wiem skąd bierze się ACK = α i CKL = α i co dalej zrobić.

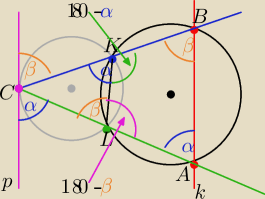
Eta: α, β kąty dopisane i wpisane Czworokąt ALKB jest wpisany w duży okrąg , to z warunku wpisania czworokąta w okrąg |<ALK|=180^o−β to |<KBA|= β i |<BKL|=180^o−α to |<BAL|=α Proste p i k tworzą z siecznymi AC i BC kąty o tych samych miarach zatem są równoległe p∥AB=k c.n.w

Michał: Dzięki wielkie. Rysunek jak zwykle genialny.

Eta: