Naszkicuj zbiór na płaszczyźnie zespolonej Łukasz: Naszkicuj na płaszczyźnie zespolonej zbiór A: A = {z∊C: π/4 ≤ Arg(z) < 3π/4 ∧ |z+2−i| ≤ 2} Jeśli dobrze zrozumiałem na ćwiczeniach to część |z+2−i| ≤ 2 jest okręgiem o środku (−2, −1) i promieniu 2. Problem mam natomiast z interpretacją i narysowaniem pierwszej części, a mianowanie π/4 ≤ Arg(z) < 3π/4.

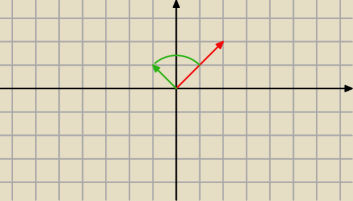
Adamm: środek okręgu jest zły interpretacja argumentu jest prosta są to wszystkie punkty należące do tego kąta

Łukasz: W takim razie, jak wyznaczyć środek okręgu?

Adamm: |z−(−2+i)| to odległość z od −2+i zatem −2+i jest środkiem okręgu

Łukasz: Już rozumiem, czyli środek jest w punkcie (−2, 1i), a wynikiem część wspólna, tak?

Adamm: jak już to (−2; 1) wynikiem jest cześć wspólna