rachunek różniczkowy Znawca: wyznacz najmniejszą i największą wartość w funkcji f w danym przedziale:

	x(x−5)2
f(x)=		, <0;6>
	x2+3

Ogólnie to doszedłem do tego momentu, że wyznaczyłem dziedzinę D_f=D_f'=R i obliczyłem pochodną. No i przyrównałem do zera. (x−1)(x−5)(x²+6x+15)=0 Wartość najmniejsza będzie w punkcie x=5, natomiast nie wiem gdzie będzie największa.

Jerzy: Pokaż tą pochodną.

Znawca:

	x4−16x2−60x+75
f'(x)=
	(x2+3)2

Przyrównałem do zera, pomnożyłem przez mianownik i podzieliłem najpierw przez (x−1), a następnie wielomian trzeciego stopnia przez (x−5). No i wyszło: (x−1)(x−5)(x2+6x+15)=0 x=1 x=5 Δ<0

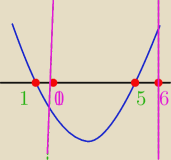
Znawca: Aaaaa, no tak. Źle rysunek zrobiłem. Przecież punkt x=0 jest po lewej x=1. No i wtedy maksimum będzie dla x=1, bo należy do przedziału